Keywords

Transition speed; Knowledge acquisition; Anthropometric parameters; Physiotherapy; Sport training

Introduction

This work seeks to answer the question of how knowledge about a biomechanical system can be acquired. Comprehending a system means to answer the following questions:

Which parameters are most closely related to certain dynamic characteristics? What are the logical connections between them? Which parameters contribute most to the dynamics of interest and how?

We provide definitions of:

• First-order parameters, which contribute most to system dynamics

• Second-order parameters, the influence of which is important but not critical

We address these questions in the context of a specific biomechanical problem, namely the prediction of the preferred transition speed (PTS) in humans, to illustrate the potential of the method.

Human locomotion is considered to take two primary forms: walking and running. Walking is a form of locomotion defined by a double support phase in which both feet are on the ground at the same time. Running is a form of locomotion defined by a double float phase. When humans run, the feet are never in contact with the ground simultaneously, and there is a phase when both feet are temporarily airborne.

The PTS is the speed at which an organism typically changes gait. Humans spontaneously switch from walking to running as speed increases; the PTS is typically around 2.0 m/s [1]. Early research indicated the ''energetic trigger'', according to which the transition minimizes metabolic costs. The predicted transitions speeds of 2.2-2.3 m/s were higher than those observed (2.1 m/s) [2,3]. Recently published investigation proposes that the transition happens as the stride frequency of walking attractor shifts slowly to the frequency of running attractor [4]. These observations seem to indicate that gait transition must be triggered by factors that are unrelated to metabolism. They could be mechanical, sensory or behavioral. Mechanical factors would prevent overloading or overexertion of structures such as bones, tendons and muscles.

The speed at which a gait transition occurs and its determinants has triggered the interest of many researches. Changing gait is not a matter of choice, but rather one of convenience, even if it remains unclear what is to be optimized. According to the inverted-pendulum model, when the centrifugal force, becomes greater than the gravitational force, mg, and contact with the ground is lost and it is no longer possible to walk [5]. Therefore, maximum walking (or transition) speed can be defined as assuming that leg length (TrH) is typically around 0.9 m for adult, PTS corresponds to 2.97 m/s, which is much higher than what was normally observed. The empirically obtained coefficient 2.2 m/s is usually used to assess PTS, and the formula is applied. What exactly contributes to the empirical value of 2.2 m/s 6 is not yet clear [6].

On the basis of a statistically derived regression model it has been suggested that lateral malleolus, thigh length and sitting height measurements are the main determinants [7]. A recent publication has reported a decreasing PTS when the feet are loaded with additional mass [8].

Several attempts have been made to describe the walkingrunning transition process based on kinematic factors, considering each mode as a non-equilibrium phase between two attractors: walking and running [9]. The synergetic model builds on acceleration of the body’s center of gravity as a primary determinant of mode shift [10].

A natural approach to solving the knowledge acquisition problem is to employ Fuzzy Set Theory, which suggests models in the form of fuzzy rule-based systems, as developed by Zadeh [11]. Fuzzy logic (FL) has already been applied successfully to a wide range of problems in various fields dealing with uncertainty and vagueness including human gait recognition [12,13]. Two main components of FL models are:

• An inference system, which provides a method for mapping input data to outputs

• A knowledge base, which represents the knowledge about a problem in the form of a collection of fuzzy rules

There are two kinds of FL-Mamdani and Takagi-Sugeno (TS) types [14].

Many research groups investigated how an optimal set of rules describing system behavior can be obtained. Three methods are available: ad hoc data covering neural networks and genetic algorithms [15-22]. Depending on the technique, the number of rules or the number of membership functions (MFs) is optimized, which might result in suboptimal solutions [23]. Although the algorithms are very sophisticated, these publications deal with predefined datasets, and selecting inputs is not the primary task. Using a Neuro-Fuzzy Designer (NFD) application which is the most common approach and which allows models to be obtained in two ways. One is clustering a large number of clusters from a dataset is organized; in other words, a large number of strongly overlapping MFs is built. The other is grid partitioning a large number of rules are generated according to the number of output clusters, using only a few input MFs. The two options entail that a rule is created for each output dataset or a cluster for one or several data input points. Since this is a black-box approach, it is difficult to gain an understanding of the underlying logic of the system under consideration (despite the high accuracy achieved), as either, the number of MFs or the number of rules is too high. Adaptive Neuro Fuzzy Inference System (ANFIS) is a recently introduced Matlab function (Matlab R2017a, MathWorks), that can partially solve the problems mentioned above [18]. The number of MFs can be defined, which automatically defines the number of rules.

An advantage of ANFIS models is that they are comprehensible. If one wants to find main determinants of the system and make out the most important parameters related to a given dynamic characteristic many can be found (Figure 3). According to Jang, “[…] ANFIS has unlimited approximation power to match any given dataset” [18]. This technique provides highly accurate models based on almost any input parameters by adjusting the shapes of input/output MFs of FL models: therefore it is difficult to identify influential parameters.

We propose a feasible approach to “zooming out” the FL models systematically with the aim of deriving generic system properties. To cope with the diversity of human body measurements, we employed FL as the core tool.

The model is sufficiently simple to allow:

• The body characteristics related to the determination of the transition speed to be identified

• Logical rules to be formulated, that provide knowledge about the biomechanical system

Methods

Fuzzy logical models description

Experimental PTS values and body parameters (Table 1) were taken from the publication.

While a variety of definitions of the term PTS have been suggested, we use that first suggested by Hreljac, who defined PTS as the average of the walk-run and run-walk transition speeds. Hreljac obtained data using a motor-driven treadmill, and the experimental protocol is described in detail [7].

First, we constructed all possible pairs and triple, quadruple and quintuple combinations of the eight body measurements shown in Table 1.

Second, we built FL models for each combination with clusters of two, three, four and five (more is also possible, but with a subject numbers of 26 larger numbers of clusters do not make sense).

We then chose the threshold accuracies. TS fuzzy if-then rules were used to build FL models [18]. The output of each rule is a linear combination of input variables plus a constant term, and the final output is a weighted average of each rule output.

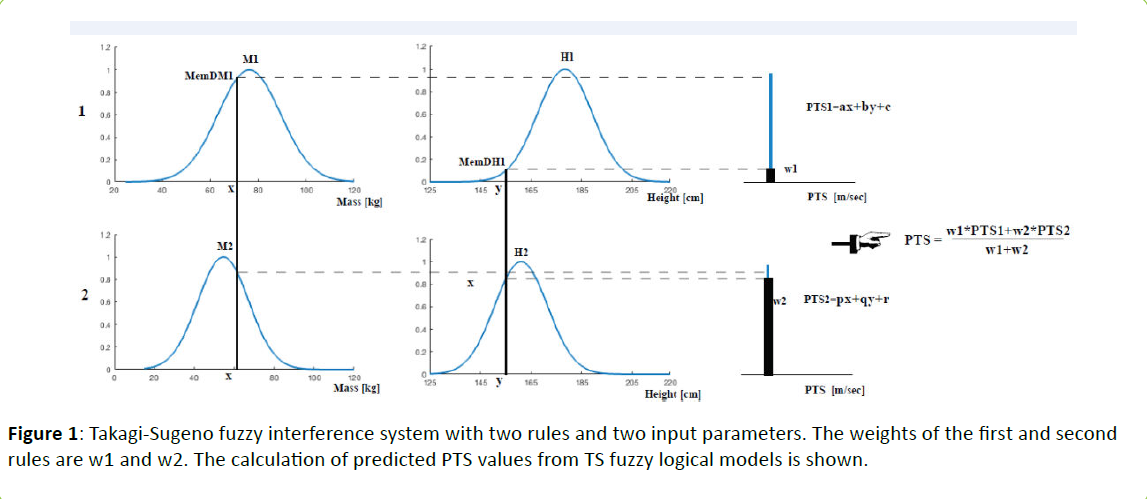
To provide a general understanding of the operation of TS inference systems with a linear output MF, we provide an explanation using the example of the following FL models.

Consider an example model with mass and height as the two input parameters and the PTS value as output. Suppose we run simulations with two clusters that produce the rule base containing two TS if-then rules:

Rule 1: If x is M1 AND y is H1, then PTS1=a.x+b.y+c (1)

Rule 2: If x is M2 AND y is H2, then PTS2=p.x+q.y+c

Where, M1 and H1 are labels of fuzzy sets characterized by appropriate MFs [11].

In Figure 1, M1 is an MF of mass, and H1 is an MF of height.

Figure 1: Takagi-Sugeno fuzzy interference system with two rules and two input parameters. The weights of the first and second rules are w1 and w2. The calculation of predicted PTS values from TS fuzzy logical models is shown.

Calculating PTS values based on the FL model requires the following steps:

• Fuzzification step: obtain membership function values of each linguistic variable. For example, if x=70 kg, the MF degree is 0.90 and y=165 cm, then the membership degree for height is 0.17 in the first rule. In the second rule, it is 0.85 for mass and 0.82 for height (Figure 1).

• Using a specific operator (AND in this case), combine the membership degrees on the premise part to obtain a weight for each rule. The weight of Rule 1 is w1=0.17, which is the logical outcome given by the AND operator or a minimum between MF degrees (MemDM1 and MemDH1 for mass and height (Figure 1). The weight output for Rule 2 is 0.82.

Generate the qualified consequent of each rule depending on the rule weight. Outcome MFs of TS fuzzy interference system are introduced by linear functions, and strictly speaking a consequent part is described by a non-fuzzy equation of input variables.

The linear functions for the first and second rules are PTS1=a.x+b.y+c and PTS2=p.x+q.y+r, respectively. The weights of rules 1 and 2 are w1 and w2, as indicated in Figure 1.

• Aggregate the qualified consequents to produce a crisp output:

TS models were obtained using the ANFIS Matlab command, therefore we call them ANFIS models, and CoreFL (Core FL) models are obtained by our technique. Both perform the same input-output data processing, as shown in Figure 1, but differ in the way in which MFs are obtained.

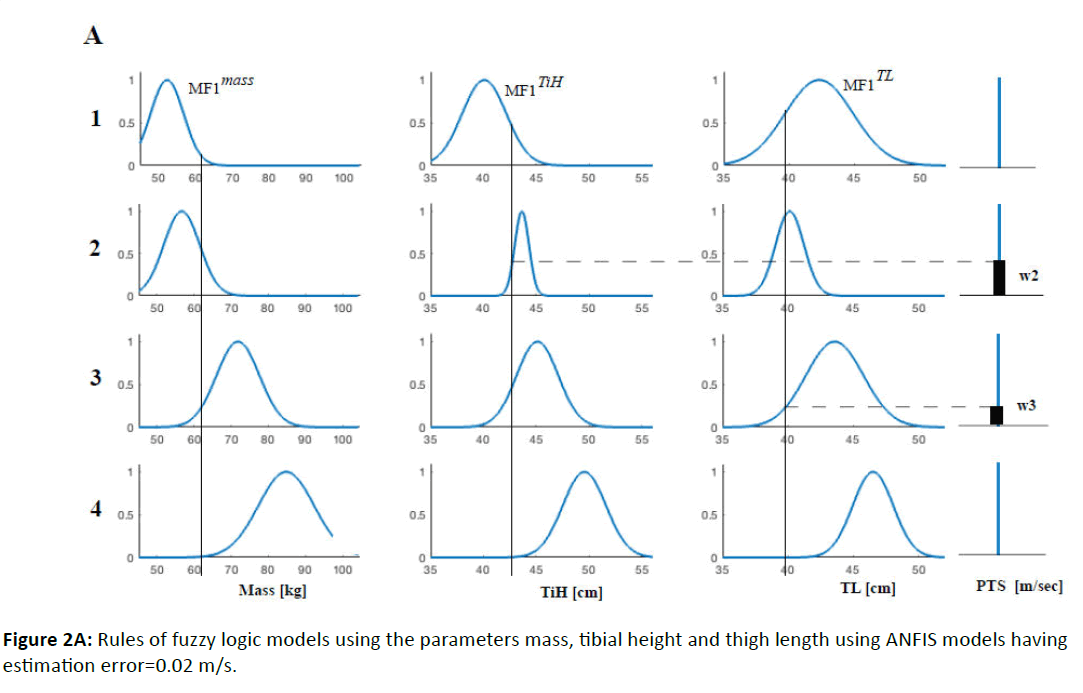
For ANFIS models, the initial FL models are created using the genfis command, which builds starting FL models (Figure 2A) based on a number of clusters defined in the form (1,3) by the user [3].

Figure 2A: Rules of fuzzy logic models using the parameters mass, tibial height and thigh length using ANFIS models having estimation error=0.02 m/s.

The ANFIS command tunes FL models to the dataset values via a hybrid learning procedure [18]. Details of the ANFIS hybrid leaning algorithm can be found in Jang et al. [18]. There were 100 optimization steps that were performed using the ANFIS command.

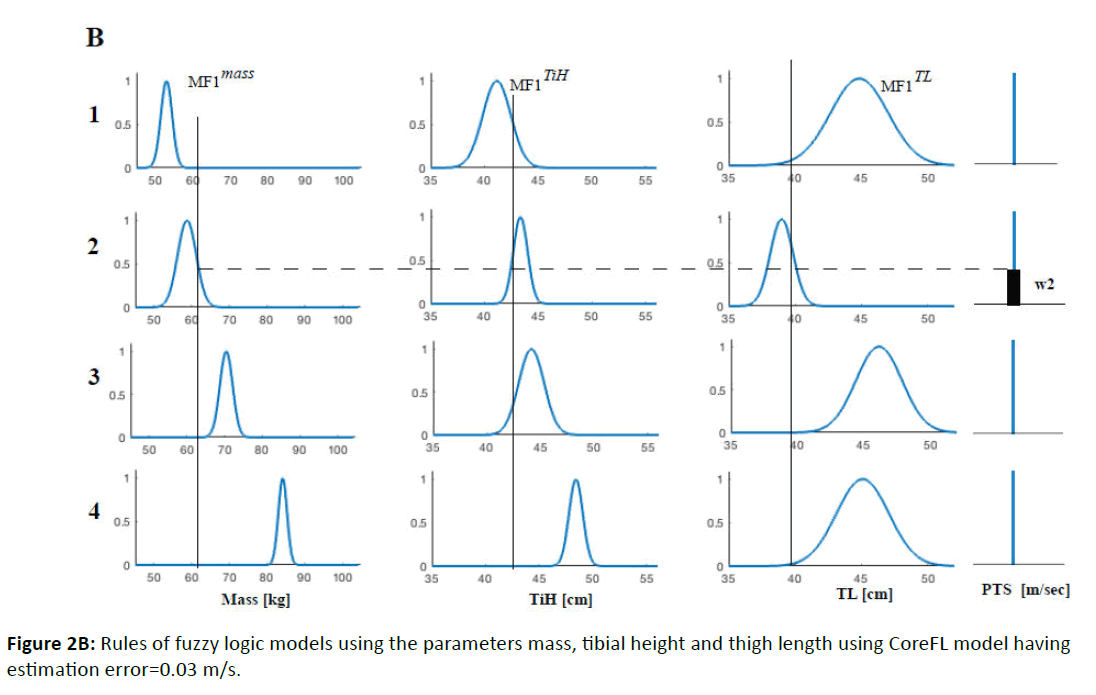
CoreFL models possess less well-tuned MFs to the data. These models were built based on clusters that are defined with stricter restraints, and only information about the cluster centers and their ranges was provided. A detailed description is given below.

In zoomed out/core FL models, clustering is performed more rigorously and MFs overlap less compared to ANFIS models and therefore only one rule has non-zero weight (Figure 2B).

Figure 2B: Rules of fuzzy logic models using the parameters mass, tibial height and thigh length using CoreFL model having estimation error=0.03 m/s.

Note that MF constructs use only the information about cluster centers and ranges and are not fit to the data.

CoreFL models were built as follows:

• Fuzzy c-means clustering was employed for every parameter combination and the number of clusters. This technique groups a dataset into n clusters, where every data point in the dataset has a certain degree to which it belongs to each cluster. Data points that are close to the center of a particular cluster therefore have a high degree of belonging or membership to this cluster, and others that lie further away from the cluster center have a low degree of belonging or membership

• The clusters were filtered to obtain smaller datasets for further MF construction as described below. Only the points with the highest membership degree to cluster i were taken to construct MFs for cluster i. For example, if point j has a membership degree of 0.6 to Cluster 1, 0.3 to Cluster 2, and 0.4 to Cluster 3, it is used to build the MF for Cluster 1 only. Hence, we performed stricter clustering

• The average, minimum and maximum of redefined clusters was calculated

• Cluster i consisted of the selected values Xj of input body measurements from Table 1.

• Input Gaussian MFs were built using

Where, is an average of and

The zooming factor (ZoomF) was chosen to be 0.4, but results remained similar for other choices 0.3, 0.5. One can vary this factor in dependence from a need getting the information and models which describe more (ZoomF is smaller) or less (ZoomF is bigger) denced points distribution around the center in the clusters.

The parameters for output linear MFs of cluster i form a vector A obtained by solving the optimization problem Such a matrix for a model as described above ( Figure 1 ) would have the form Even though we obtained parameters of output MFs by optimization, the model predictions were calculated with input membership function degrees that were not optimized to the input data. Employing different shapes of input MFs based on clusters range one can obtain additional knowledge about data distribution in the clusters.

For example, if triangular or bell-shape MFs suggest models with better estimation one can conclude that the data distribution is closer to these shapes.

The standard deviation (SD) was calculated using

Where, PTS_n is the value obtained for subject n in experiments (Table 1), FLM is the prediction of the FL model, and N is the size of the set of experimental values (26 points).

Threshold error criteria

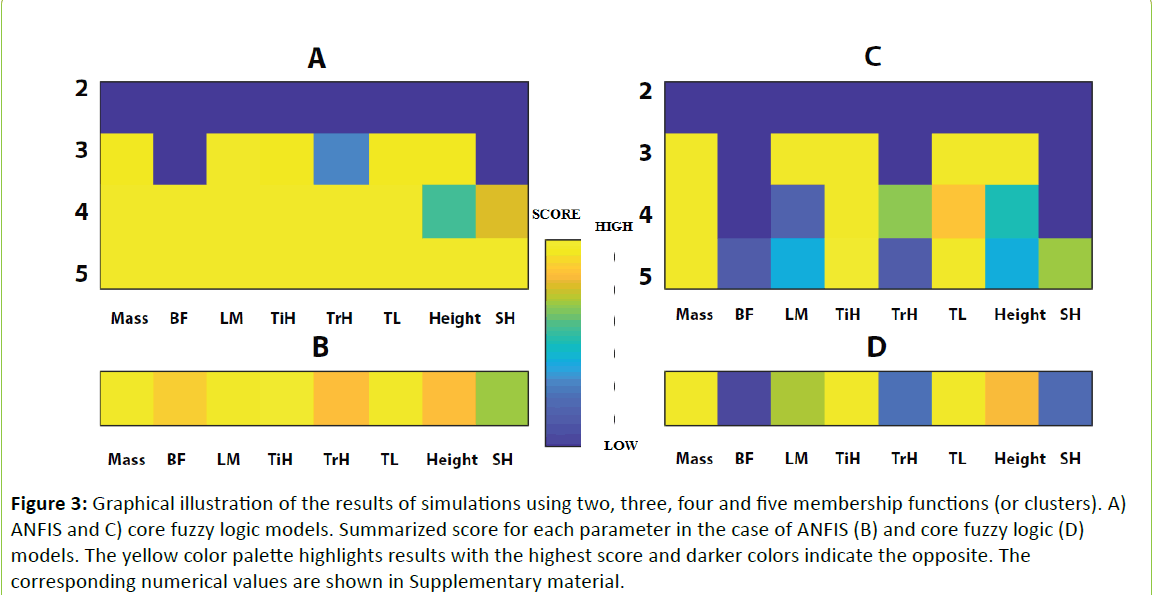
Figure 3 shows the combined results from simulations with different parameters. We employed two criteria:

Figure 3: Graphical illustration of the results of simulations using two, three, four and five membership functions (or clusters). A) ANFIS and C) core fuzzy logic models. Summarized score for each parameter in the case of ANFIS (B) and core fuzzy logic (D) models. The yellow color palette highlights results with the highest score and darker colors indicate the opposite. The corresponding numerical values are shown in Supplementary material.

• Pre-established error (0.07 m/s):

If model precision is higher, then the model is discarded, which is why Figure 3A (case of two clusters) shows no successful models and no parameters are highlighted.

Minimum error of the most successful model: Models whose estimation deviates by less than 15% from the minimum error of the most successful model are considered. The results for four clusters can be found in Table 2.

Methods limitations and perspectives

In general, the methodology is aimed to be employed for problems with a dataset where a number of interconnected variables are present, so the data acquisition becomes a rather tedious process. Therefore, further experiments are needed to be designed consciously. These situations are often in biology.

For such cases, it is feasible to build testable hypothesis by extracting the logical rules refer to different criteria-varying type of MFs and its parameters, for example, a zooming factor.

The highest score as defined by threshold error criteria get models which possess largest number of well-defined (that is, well packed and equally distributed around the center) clusters connected by logical operation “AND”. One of the outputs is the number of clusters for which this is the case.

If one seeks to find models with high density data in attributed clusters, one can employ the zooming factor 0.1-0.2. Since it is almost impossible to have data that ideally satisfy the criteria of a well-defined cluster, the highest score obtain those models which include most of such clusters or which data have a closest distribution to the demanded criteria introduced by MFs of CoreFL models.

Illustrating models as shown in the Figure 1* in Supplementary material one can conclude, for example, which rules are more valid based on the current dataset. On the Figure 1*(supplementary material) one can see that cluster 2 (mf2 or rule 2) has only a few number of points (two points) in comparison with other clusters. Therefore, the clusters (or rules) one, three and four are more valid. To validate the rule two ideally, on needs to get new statistics on this range of data from new experiments. Nevertheless, for the present dataset such a model gives the best prediction.

One can suggest that taking the densest region in the clusters as the centers of MFs for CoreFL models would bring better estimation of PTS. The aim here was to build MFs unbiased to data and therefore only the clusters range and its center (C_i) were employed.

Results

Two practical questions that arise when general rules underlying a system are to be found:

1) What are the main (two, three, and four) parameters (determinants) that have the greatest influence on system behavior?

2) What are the primary rules or tendencies in the systems that define its logic? We suggest several main determinants for PTS and provide some primary rules with a prediction error comparable to those of other methods. The models that satisfy these criteria offer comprehensible knowledge about the system. In our case, a table of subjects’ body measurements was the starting point for answering these questions. The PTS values obtained are presented in Table 1.

To build FL models, we first ran simulations employing the ANFIS method. The colors in Figure 3 indicate how often a parameter participated in successful models that satisfied the threshold criteria. As can be seen in b mass, LM, TiH, TL and body height had the highest scores in simulations with three MFs. It is indicated in the second row of Figure 3A since the number of MFs is equal to the cluster number.

For four MFs, six parameters out of eight can be considered as influential (refer to threshold error criteria, see Methods), and in the five-cluster case, the whole parameter set is highlighted (Figure 3A).

Based on the simulation results (Figure 3A), one can identify system determinants by applying various criteria. We suggest summing the scores obtained from successful models for all clusters and for each parameter.

This means aggregating the scores over each column (each parameter) in the result matrix (Table 1 in the Supplementary Material). The results are shown in Figure 3B: four parameters out of eight contributed significantly. This indicates that mass, LM, TiH and TL fulfill the formal criteria to be system determinants, although trochanteric and sitting heights also score highly.

The ANFIS method has the property of “[…] unlimited approximation power to match any given dataset”18, this conclusion may be fallacious. The concern is the following: Models are obtained by parameter fitting of MFs to the dataset (Table 1), yielding low estimation errors with a variety of parameter combinations, which is reflected in a large number of successful models obtained (see the list of models obtained in the case of four clusters in the Supplementary Material).

Hence, we suggest recasting the results using a different approach that can be considered a “zoom out” of ANFIS models. MFs built by the methodology proposed below overlap less, and therefore the FL models are in a sense less fuzzy.

We built models that are less “tuned” to the dataset. We call these models CoreFL, since MFs hardly overlap and based on cluster center and range only (Figure 2).

With the help of CoreFL models, influential parameters can be identified more easily, and the results from ANFIS modeling can be corroborated or disproved. Note that the precision of successful CoreFL models does not deviate much from that of ANFIS FL models, but the number of models that satisfy the threshold criteria is smaller due to their more generic nature (see results for four clusters in Table 2 with CoreFL models.

One can compare the results with ANFIS successful models in the Table 2* of Supplementary material).

For example, the ANFIS model with mass, TiH and TL had an estimation error of 0.02 m/s, while the CoreFL model had 0.03 m/s (Figure 2, Table 2).

The results are illustrated in Figures 3C and 3D. They indicate that the output linear membership functions for each rule relate rather to the cluster ranges than to the data specifically. The matrix of the numerical values illustrated in Figures 3C and 3D can be found in the Supplementary Materials (Table 1B).

To clarify how we obtained the color maps, Table 2 shows the simulation results for four clusters of CoreFL models. Scores for these models are illustrated in the fourth row in Figure 3C.

Table 2 presents how the summarized score and the color for each parameter were obtained. Based on the CoreFL models, the system determinants are mass, TiH and TL and can be thus called first-order parameters (Figure 3D).

One can also track first-order parameters as the cluster number increases. They stay conserved in the different parameter combinations (this is also the reason why these parameters appeared to have a highest score). In Table 2, mass, TiH and TL occur in all parameter combinations.

When simulations were run:

• with pairs, successful models were obtained for: mass+TiH and mass+TL

• with three parameters: mass+TiH+TL

• with four clusters: mass+TiH+TL+either LM or height

Last two additional parameters increase model accuracy and can therefore be called putative second-order parameters (the additional parameters appear most often in successful models with more than three inputs).

The models obtained have, as shown below, the following set of rules for models with four MFs and four rules.

For example, the model for mass, TiH and TL (Figure 4) is:

Figure 4: Depiction of models having four MFs and four rules.

A graphical representation of ANFIS and CoreFL rules for mass, TiH and TL is illustrated in Figure 2. It can be seen that in many cases the core MF (Figure 2B) has narrower MFs due to stricter cluster membership criteria and can be written following way(Figure 5):

Figure 5: Illustration of narrower MFs due to stricter cluster membership criteria.

MFs parameters for CoreFL and ANFIS models from the Figure 2 are given in the Supplementary material.

To gain an understanding of the system, the principal laws can be formulated by reading the graphical rule representation of the core FL model (see Supplementary Material). The first two rules suggest that objects with a low mass (<60 kg) and short tibial height (<44 cm) have a tendency towards lower transition speeds ≈ 2 m/s. The PTS seems to be independent of thigh length, since the range of its MFs is very broad. The fourth rule suggests that people with a high mass (≈ 85 kg), long tibial bone (≈ 50 cm) and average thigh length have a relatively high PTS value ≈ 2.2 m/s. Objects with average mass (≈ 70 cm), tibial height (≈ 44 cm) and long thigh length have a PTS ≈ 2.15 m/s (third rule). These formulations describe only tendencies, which one can see by varying parameters around MF centers. Varying the values more exact gives more precise prediction.

How strong ANFIS and CoreFL models relate to the data can be seen in Figures 6 and 7.

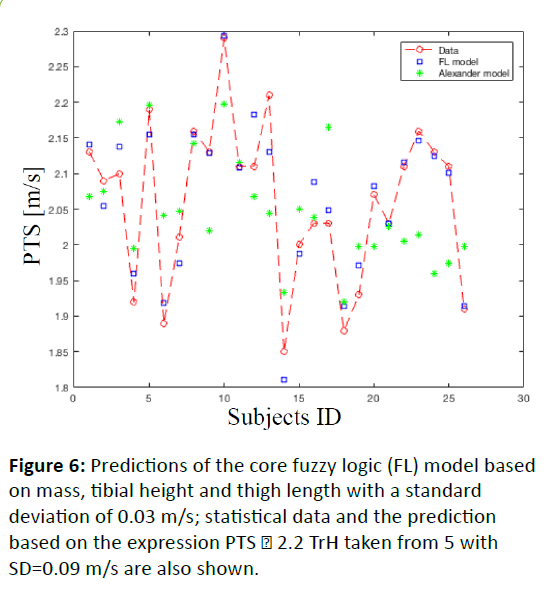
Figure 6: Predictions of the core fuzzy logic (FL) model based on mass, tibial height and thigh length with a standard deviation of 0.03 m/s; statistical data and the prediction based on the expression PTS  2.2 TrH taken from 5 with SD=0.09 m/s are also shown.

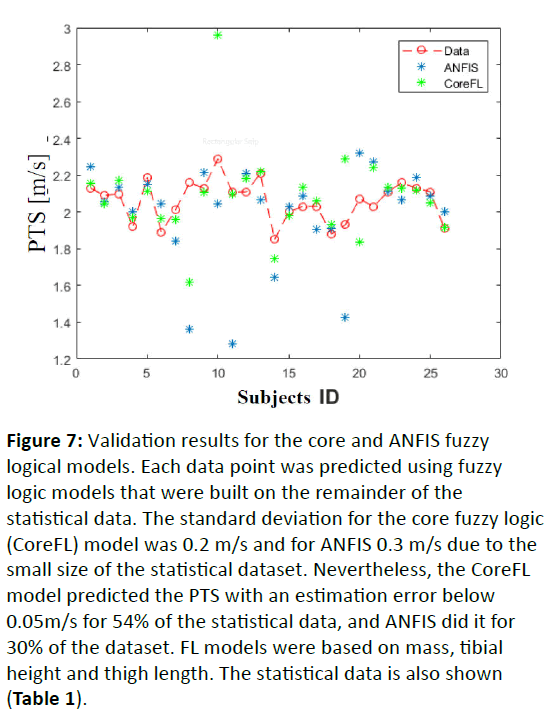
Figure 7: Validation results for the core and ANFIS fuzzy logical models. Each data point was predicted using fuzzy logic models that were built on the remainder of the statistical data. The standard deviation for the core fuzzy logic (CoreFL) model was 0.2 m/s and for ANFIS 0.3 m/s due to the small size of the statistical dataset. Nevertheless, the CoreFL model predicted the PTS with an estimation error below 0.05m/s for 54% of the statistical data, and ANFIS did it for 30% of the dataset. FL models were based on mass, tibial height and thigh length. The statistical data is also shown (Table 1).

In Figure 6, the predictions of CoreFL models for mass, TiH and TL are shown. Figure 7 presents the predicted PTS values when ANFIS and CoreFL were obtained excluding the data point being predicted, which means that each time the FL models were trained on a new dataset consisting of 25 data points. The results show that for ANFIS models 30% and for CoreFL 54% of the predicted PTS values achieved an estimation error below 0.05 m/s. In general, CoreFL predictions are close to the statistical data, as can be seen in Figure 7. These simulations show that CoreFL is less sensitive variations to the statistical data.

A possible alternative approach to detecting the determinants is Principle Component Analysis (PCA). This suggests PCA1=-0.684Mass-0.323TrH-0.564Height-0.25SH and PCA2=0.939 BF as first and second PCA. Employing PCA1 and PCA2 as inputs to the FL model yields 0.07 m/s when using CoreFL models and 0.05 m/s when using ANFIS FL models. The variables suggested by the PCA method were therefore not considered.

Discussion

The main issue addressed in this work was how-from a number of anatomical parameters-detect those that relate most to the dynamical characteristic of interest. This is part of the larger task of acquiring knowledge about a system. We addressed this question in the context of a biomechanical system. We consider our approach useful in practice, as it provides a simple assessment of the factors that are most involved in a specific dynamic activity. Our approach cannot only be applied to body parameters, but also to any measurements that are related to a movement under investigation.

In this work, we applied our technique to the PTS problem. Investigating this initially apparently simple-problem, one can consider multiple factors that influence the dynamics, such as individual variability in the human skeleton, training experience, age and even emotional state. All these factors make accurately predicting human dynamics difficult and the problem fuzzy, a characteristic of all biological systems.

Our results indicate that mass, tibial height (TiH) and thigh length (TL) are first-order determinants of the PTS. The secondorder determinants are presumably lateral malleolus height (LM) and body height. Our findings partially corroborate earlier theoretical findings which suggest the following PTS determinants: trochanteric height or thigh length, sitting height (SH), lateral malleolus height [5,7]. A comparison of the predictions presented in these publications to those of FL models based on the first-order determinants is given in Figure 6. The CoreFL model estimation error is 0.03 m/s, that of Alexander’s model 0.09 m/s and that based on Hreljac’s regression equation is 0.10 m/s [7]. A low estimation of the obtained CoreFL models approves its validity.One can see that despite its simplicity the model of inverted pendulum predicts PTS values rather well [5]. Since, Our models agree most with Alexander’s model and reflect that the ratio between TiH and TL can define the PTS [5]. We also assume that the empirically offered coefficient 2.2 m/s6 can originate from the mass value as it is suggested by our models [6]. Mass parameter has the highest score (Table 2).

The indication of mass as a new main determinant is supported by recently published experimental data [8]. It has been shown that the mass loading on the feet lowers the transitional speed. Our results obtained on the basis of a statistical set indicate the opposite. There is a tendency towards an increased PTS as mass increases. However, the body proportions here have a tendency to increase along the mass in the dataset (Table 2) which differ from those in the experiments of MacLeod et al. where additional mass was introduced on the feet [8]. To our knowledge, our model is the first to include mass in predicting PTS (Figure 2B). The defined determinants suggest that a physical model based on coupled oscillators with lengths of TiH, TL and distributed mass over limbs could be a good option. By means of such a model the influence of an additional mass, introduced on the body’s center or feet, would indicate how the PTS depends on mass location. Then the above comparison can be made more rigorously.

In the work of Zielinska et al. walking trajectories were generated by coupled Van-der-Pol oscillator [24]. It was shown that oscillators’ parameters, which are indirectly related to the mass, generate different joint angular velocities and therefore different gait trajectories. However, the influence of a mass location for PTS case is to our knowledge not investigated enough and can be a matter of a future research. It was shown in a number of works that an additional mass changes the gait patterns [25-29].

More importantly, we provide a basis for discussing this issue and mean of comparing the tendencies of various subject groups using validated models. Based on our predictions, we argue that the proposed approach allows comprehending system behavior suggesting system determinants and logical rules in the form of FL model. Moreover, one can design more efficiently further experiments based on obtained models.

As mentioned above, ANFIS FL models can be tuned to the dataset with very high precision. Distinguishing between influential and non-influential parameters is therefore difficult, since small estimation errors can be achieved for a large number of parameters and their combinations. To overcome this problem, we have proposed an approach to making predictions less independently of precise data. The “zoomed out” or CoreFL models suggested here instead are based on cluster range and are therefore more general.

The concept of core FL models becomes clearer when considering the following example: Imagine a detailed portrait of a person. Applying our approach, we seek to draw a less detailed sketch by extracting the main features and logical rules between them. Ideally, the rules could be applied to any portrait, and therefore rules incorporate an understanding of how to draw a sketch from a photo while keeping its subject recognizable.

The Greek philosopher Plato suggested that knowledge is more than just information and data, and comes from how to ask and answer questions. Our approach seeks to answer the question of what are the main system determinants and to detect logical connections between them, thus giving rise to hypotheses that can potentially be further transformed into analytical models. This advantage of our approach could also be put to use in other biomechanical applications, for instance, in detecting harmful patterns in movement in physiotherapy or sports.

Conflict of Interest

Authors declare there is no conflict of interest.

Acknowledgement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

We thank Alexander Vereshchaga at National Research Nuclear University MEPhI for multiple fruitful discussions throughout this work.

Ingrid Abfalter served as an editor.

References

1. Saibene F, Minetti AE (2003) Biomechanical and physiological aspects of legged locomotion in humans. Eur J Appl Physiol 88: 297-316.
2. Falls HB, Humphrey LD (1976) Energy cost of running and walking in young women. Med Sci Sports 8: 9-13.
3. Margaria R (1976) Biomechanics and energetics of muscular exercise. Oxford: Clarendon Press.
4. Hansen EA, Kristensen LAR, Nielsen AM, Voigt M, Madeleine P (2017) The role of stride frequency for walk-to-run transition in humans. Sci Rep 7: 2010.
5. Alexander RM (1996) Walking and Running. The Mathematical Gazette 80: 262.
6. Vogel S (2013) Comparative biomechanics: Life's physical world/Steven Vogel, Oxford: Princeton University Press. Princeton, New Jersey.
7. Hreljac A (1995) Effects of physical characteristics on the gait transition speed during human locomotion. Human Movement Science 14: 205-216.
8. MacLeod TD, Hreljac A, Imamura R (2014) Changes in the preferred transition speed with added mass to the foot. J Appl Biomech 30: 95-103.
9. Diedrich FJ, Warren WH (1995) Why change gaits?: Dynamics of the walk-run transition. J Exp Psychol Hum Percept Perform. 21: 183-202.
10. Abdolvahab M (2015) A synergetic model for human gait transitions. Physica A 433: 74-83.
11. Zadeh LA (1965) Fuzzy sets. Information and control 8: 338-353.
12. Viteckova S, Kutilek P, Kauler J, Svoboda Z (2014) Fuzzy expert system for determining the human gait phase. International conference on applied electronics (IEEE) pp: 315-318.
13. Computational intelligence, cyber security and computational models (2015). Springer Berlin Heidelberg, New York.
14. Jang JSR, Sun CT, Mizutani E (1997) Neuro-fuzzy and soft computing: A computational approach to learning and machine intelligence, MATLAB curriculum series. London: Prentice Hall, Upper Saddle River, New Jersey.
15. Wang LX, Mendel JM (1992) Generating fuzzy rules by learning from examples. IEEE Trans Syst Man Cybern Syst 22: 1414-1427.
16. Nozaki K, Ishibuchi H, Tanaka H (1997) A simple but powerful heuristic method for generating fuzzy rules from numerical data. Fuzzy Sets and Systems 86: 251-270.
17. Shann JJ, Fu HC (1995) A fuzzy neural network for rule acquiring on fuzzy control systems. Fuzzy Sets and Systems 71: 345-357.
18. Jang JSR (1993) ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans Syst Man Cybern Syst 23: 665-685.
19. Thrift PR (1991) Fuzzy logic synthesis with genetic algorithms. InICGA pp: 509-513.
20. Liska J, Melsheimer SS (1994) Complete design of fuzzy logic systems using genetic algorithms. In: Proceedings of the third IEEE Conference on Fuzzy Systems, IEEE world congress on computational intelligence, pp: 1377-1382.
21. Gonzalez A, Perez R (1998) Completeness and consistency conditions for learning fuzzy rules. Fuzzy Sets and Systems 96: 37-51.
22. Cordón O, Herrera F (1997) A three-stage evolutionary process for learning descriptive and approximate fuzzy-logic-controller knowledge bases from examples. Int J Approx Reason 17: 369-407.
23. Gervasi O, Kumar V, Tan CJK (2006) Computational science and its applications (ICCSA) In: Proceedings of Springer Berlin Heidelberg, International Conference, Glasgow, UK p: 5.
24. Zielinska T (1996) Coupled oscillators utilised as gait rhythm generators of a two-legged walking machine. Biol Cybern 74: 263-273.
25. Mei Q, Gu Y, Fernandez J (2018) Alterations of pregnant gait during pregnancy and post- partum. Sci Rep 8: 528.
26. Selles R, Bussmann J, Van Soest AK, Stam H (2004) The effect of prosthetic mass properties on the gait of transtibial amputees--a mathematical model. Disabil Rehabil 26: 694-704.
27. Sheehan KJ, Gormley J (2013) The influence of excess body mass on adult gait. Clin Biomech (Bristol, Avon) 28: 337-343.
28. Blickhan R (1989) The spring-mass model for running and hopping. J Biomech 22: 1217-1227.
29. Silvernail JF, Milner CE, Thompson D, Zhang S, Zhao X (2013) The influence of body mass index and velocity on knee biomechanics during walking. Gait Posture 37: 575-579.