Mini Review

This note presents a summary of the vagaries of Action Principles in the context of Thermodynamics, an account of my paper in Entropy of 2011, and references to more recent developments.

Action Principles have played an important role in Physics, but not in all branches.

Some of the leading physicists of the 19th Century tried very hard to cast Thermodynamics in the mold of Lagrangian Mechanics, formost among them Hermann Helmholtz, Joshua Gibbs, Henri Poincare, Pierre Duhem and James Clerk Maxwell. Maxwell was impressed by Gibbs’ work (1878) and was fully engaged in a search for an action principle when he died.

Today, Thermodynamics is seen as being largely defined by two dif- ferential equations. There are several formulation but the one we shall use was the work of Helmholtz. It concentrates the attention on the Helmholtz Free Energy F (V, T) and on the following equations

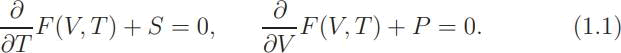
The entropy plays a relatively minor role here, and for Helmholtz that was a large advantage, for entropy was at that time, as it is today, a very difficult concept. The unusual property of entropy seemed to make difficult its incorporation into a Lagrangian framework.

If we put those considerations aside, and ask whether the two equa- tions in (1,1) are the Euler-Lagrange equations of an Action A(V, T, S, P ), then the answer is easy to find:

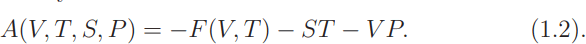
The variation must be carried out with S and P fixed. Here we have a theory based on 4 variables; the essential point is that all of them are independent variables, in the formula and in the variational principle; they are the “off-shell” variables. In1this context the entropy is defined in terms of F by the first equation in (1.1).

Review of the paper “Heat and Gravity”, Entropy 2011, , by the author, Copy- right 2021 by Christian Fronsdal.

Defined by (1.2) is global thermodynamics, the thermodynamics of a spatially uniform systems in equilibrium. There is more to thermo- dynamics than that; most important, the systems have kinetic degrees of freedom. Thermodynamics must be integrated with Hydrodynamics. The paper under review was inspired by the realization that both need to be combined with Relativity, Special and General.

Einstein created the theory of General Relativity on the concept of coordinate invariance and found the action that allows to calculate the metric and the motion of point particles. Unlike Special Relativity the general theory has never been fully integrated with other branches of physics, especially not with thermodynamics and hydrodynamics, as can be shown as follows.

The most popular and the most advanced version of non relativistic hydrodynamics is based on the action found by Lagrange in 1760:

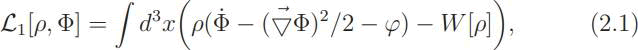
where the gradient −∇Φ is the velocity and ϕ is the Newtonian potential of gravity. All evidence that Newtonian gravity is the non-relativistic limit of General Relativity comes from the physics of particles. Until recently there was no generally relativistic hydrodynamics that could be compared with this classical theory. The Newtonian potential was included in (2.1) by analogy with particle physics.

All of modern, relativistic particle theory can be integrated with General Relativity, all of the resulting relativistic field theories possess non relativistic limits, but none of these non relativistic limits contain the Newtonian potential! Can this situation fail to convince us that something remains to be done?

In a precursor to the paper under review a special case was discovered. Consider the scalar, Klein-Gordon field ψ and the Lorentz invariant Lagrangian density,

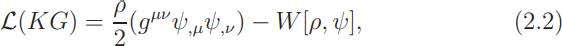
where (g^μν) is the Lorentz metric, upgraded in a special case to

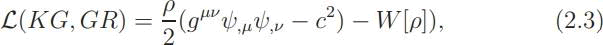
where (g_muν) is a general, Riemannian metric.

The density factor ρ is unconventional in both, except in the case that it is a constant. It is needed in the non-relativistic limit where the density is an essential variable. This limit exists in the form of an expansion in powers of 1/c:

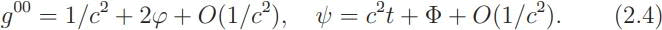
The terms of order c² cancel and there remains the action of Lagrange, including the Newtonian potential Φ ! In (2.2) and (2.3) a mass term may be included in the potential W , or it may be added as a Lagrange multiplier. This is the only known relativistic field theory that includes the Newtonian potential in the non relativistic limit. The inclusion of the density as a kind of primitivity is the key. It provides a glimpse of a future theory that integrates General Relativity with Hydrodynamics, it stimulates a new approach to Hydrodynamics and, inevitably, to Thermodynamics. It was the inspiration for embarking on a program to understand thermodynamics and for the paper under review.

In local thermodynamics the function F in Eq.(1.2), Helmholtz’s free energy, is the integral over space of a free energy density f (ρ, T ). We interpret F as the free energy per mol or per gram, then and the stationary action is

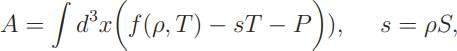
where S is the specific entropy density, the entropy per gram or per atom. To this we must add the kinetic energy ρv²/2,

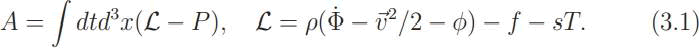
Addition of the term ρΦ produces the action found by Lagrange for the case of of an irrotational vector field v = −∇Φ. Variation of (3.1) with respect to the density ρ gives

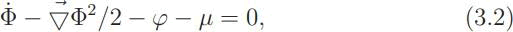
whereµ = ^∂ f (ρ, T ). We shall show that this is the Bernoulli equatio (1738) of hydrodynamics.

Theorem. If the specific entropy density S is uniform, then the internal energy density u(ρ, s) = f (ρ, T )+sT has the following properties

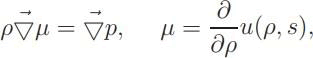
where p is the thermodynamic pressure

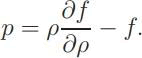
In that case the Euler - Lagrange equation that comes from variation of the action (3.1) with respect to the density is the Bernoulli equation

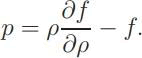
The integration of Hydrodynamics and Thermodynamics is thus complete, in this particular case. Unfortunately, the restriction

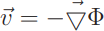
is very strong.

The nemesis of Helmholtz and his colleagues was that the entropy did not fit the scheme of Lagrangian structural dynamics; apparently they took it for granted that the entropy should be one of the canonical variables. This difficulty may be related to another one, of recent date. In a Lagrangian system the Euler-Lagrange equations guthat st arantee ationary solutions are minima of the Hamiltonian. In the case that the

Lagrangian is of the form (3.1), the Hamiltonian density is the internal energy density

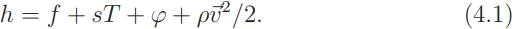
This is the Legendre transform of the Lagrangian. In a standard Lagrangian theory the Hamiltonian has an important property: the ground states are characterized as minima of the Hamiltonian H = ∫d³xh.

But the systematic investigation by Callen has shown that, for sta- tionary states in the absence of gravity, it is not the integral ∫d³(f + sT ) that has this property, but ∫d³xf . The error arises from the fact that our Action is degenerate; the variables S and T do not form a canonical pair.

This may be what has prevented Callen (and Helmholtz) from recognizing a Lagrangian underlying his system of equations. And we are in the same difficulty since our identification of the Hamiltonian density with the internal energy density is wrong. Once recognized, this defect can now be repaired.

A slight change of notation will do it; replace the variable S by the variable σ, according to

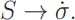
This has the effect of removing the term sT from the Hamiltonian. In the Lagrangian replace

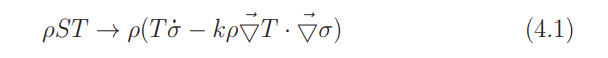
with k constant. Now we can promote σ to a canonical variable, with canonical conjugate kρT . The variational equations remain the same, except for a new Euler - Lagrange equation, from variation of σ, namely

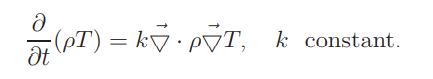
The equations of motion include the Fourier heat equation and the canonical system is non-degenerate. Note that S, under its new name, retains all the classical attributes. This includes the “always increase” property postulated by Clausius and proved by Gibbs under conditions that are valid within the variational framework. And finally, the canonical Hamil- tonian is now the free energy; it includes a term kρ(∇T · ∇σ), instead of sT.

The new expression for the total Lagrangian is

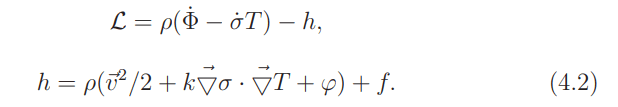
The Hamiltonian energy appears amplified by the heat energy ∫ d³xρsT , a term that is attributable to Dark Matter. The total energy is

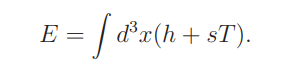
Including the heat energy will help to explain the expansion of the universe

The integration of irrotational hydrodynamics with thermodynamics makes urgent the generalization of hydrodynamics beyond irrotational velocities. So far we have followed the trend of classical applications of hydrodynamics, adopting the Lagrangian found by Lagrange with the limitation to irrotational velocity fields. This is not the popular explanation of the meniscus seen in a glass of water that is placed on the center of a turn table. Here, the usual explanation would rely on an- other Lagrangian, as old as that a of Lagrange and usually attributed to

Euler

(5.1)One difficulty is that in this case there is no justification for including the Newtonian potential. (The approach to hydrodynamics that is based on the Navier - Stokes equation combines solutions of both theories while ignoring the Euler-Lagrange equations of both.)

Landau was the first to speak for the existence of two vector fields, using the solutions of both, phonons for the irrotational modes, rotons for the other, although he never acknowledged the connection between (5.1) and his rotons. Early attempts to construct variational equations for super fluids, including the first one by London (1950), simply added the two Lagrangians, ignorong the irrotational restriction as well as the equation of continuity).

The fact that (5.1) contains a vector field, like electrodynamics, should have been a warning that the complete, Lorentz invariant version is a gauge theory. The relativistic extension was discovered by Rascetti and Regge (1973). That war 33 years after Landau’s proposal and 10 years after the relativistic gauge theory was described by Ogievetskij and Pol- ubarinov. There was a serious attempt by Seliger and Whitman (1968) but it did not embrace relativity

The natural dynamics of 2-vector, conservative hydrodynamics is found to be a combination of the two Lagrangians in (2.1) and (5.1).

The field ^∙ X is strongly constrained; nevertheless it provides the extra variables that are needed for fluid stress. As a vector field it supplies the spin that is needed for applications to Superfluids and to Gravitational Waves. The theory has been applied to several problems, listed here.

Stability analysis of cylindrical Couette flows (2020b). Newtonian theory of rotating Planets (2021a). Metastabile fluids, capillary action and Superfluids (2021b). Hydrodynamic sources of Gravitational Waves (2021c). Under the meniscus, a physical theory of capillary effect (to be published). Hydrodynamic Drag” (in progress).

References

1. Bernoulli, D., Argentorat (1738)
2. Callen, H.B., Thermodynamics, Wiley, New York (1960)
3. Clausus, R. “Abhandlungen Uber die Mechanische Waemetheorie”, Friedrichs Verlag 1864
4. Duhem, P., “Sur les equations generales de la Thermodynamiques”, Annales scientifiques de l’Ecole Normale Suprieure,Ser. 3, 8 (1891), p. 231-266
5. Einstein, A., “The Principle of Relativity”, Sitz.Preuss. Akad. Wiss.142 (1917)
6. Fronsdal, C. “Ideal stars in General Relativity”, Gen. Rel. Grav 39, 1971-2000 (2007)
7. Fronsdal, C. , “Heat and Gravitation. I. The action Principle”, Entropy 16(3), 1515-1546 (2011)
8. Fronsdal, C. Adiabatic Thermodynamics of Fluids. From Hydrodynamics to General Relativity, World Scientific (2020a)
9. Fronsdal, C., “Stability analysis of Cylindrical Couette flow”, Physics of fluids 2020b.
10. Fronsdal, C., “Newtonian theory of rotating Planets”, to be published 2021a
11. Fronsdal,C., “Metastable fluids, Capillary action and superfluids”, to be published 2021b.
12. Fronsdal, C., “Hydrodynamical sources for Gravitational Waves”, to be published 2021c
13. Fronsdal, C.,“Under the meniscus, a physical theory of capillary effects”. to be published.
14. Fronsdal, C.,“Drag by hydrodynamics.” to be published.
15. Gibbs, J.W., “On the equilibrium of Heterogeneous Substances”, Trans. Conn. Acad. (1878)
16. Helmholtz, H., “On the Conservation of Force”. translation by Tyndall, J., Science Memoirs, lpndon .
17. Lagrange, J.M., Taurinensia, ii. 1760, (Oeuvres, Paris 1867,1892) Landau, L., “Theory of Superfluidity in Helium II”,
18. Rev. 60 3e6-358 (19410
19. London, F., “Superfluids”, vol 2, page 128, Dover Publications , 1950 Maxwell, J.C., “On the dynamical Theory of Gases”, Mag. J. Sci.35 185-217 ,1868
20. Poincare, H., “Thermodynamique”, Gaut1908ier-Villars 2 Ogievetskij, V.I. and Polubarinov, I.V.,“Minimal interactions between spin 0 and spin 1 fields”,J. Exptl. Theor. Phys. (USSR) 46, 10481055 (1964)
21. Rasetti, M and Regge, T. , “ Quantum vortices and diff (R3)”, in
22. Lecture Notes in Physics, Volume 20. Physica 80 A, 217 (1973) Seliger, R.L. and Whitman , G.B., “Variation principles in continuum mechanics”, Proc.Roy.Soc., A 305,1-25 1968.