A Weighted Cosine RBF Neural Networks
Muhammad Moinuddin1,2, Imran Naseem3,4, Wasim Aftab1, Sidi A Bencherif5,6,7 and Adnan Memic1
1Electrical and Computer Engineering Department, King Abdul Aziz University, Saudi Arabia
2Center of Excellence in Intelligent Engineering Systems (CEIES), King Abdulaziz University, Saudi Arabia
3School of Electrical, Electronics and Computer Engineering, University of Western Australia, Australia
4College of Engineering, Karachi Institute of Economics and Technology, Karachi, Pakistan
5Laboratory of Biomechanics and Bioengineering (BMBI), Sorbonne Universities, University of Technology of Compiègne (UTC), Compiègne, France
6Harvard John A Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, USA
7Department of Chemical Engineering, Northeastern University, Boston, MA, USA
- *Corresponding Author:
- Adnan Memic
Center of Nanotechnology
King Abdul Aziz University, Saudi Arabia
Tel: 617-373-4495
E-Mail: amemic@kau.edu.sa
Received Date: May 09, 2017; Accepted Date: May 17, 2017; Published Date: May 25, 2017
Citation: Moinuddin M, Naseem I, Wasim A, et al. A Weighted Cosine RBF Neural Networks. J Mol Biol Biotech. 2017, 2:2.
Abstract
Over the past decade, the field of bioinformatics and computer modeling applied to biological challenges has been growing exponentially. Many approaches have been developed that tackle applications ranging from protein classification, structure prediction to disease prediction. This work focuses on the design of a novel kernel for the Radial Basis Function Neural Networks (RBFNN). The proposed kernel is based on weighted cosine distance between the input vector and the center vectors associated with RBFNN. The weighting is introduced in: i) the inner product of input and neuron’s center, ii) norm of the input vector, and iii) norm of the center vector. We demonstrate how the weighting matrix can be chosen for different applications to optimize the performance of the WC-RBF. As case studies, we present the PDZ domain classification and the channel estimation problem with correlated inputs. We also design an adaptive technique to update the weighting matrix for an arbitrary data using the approach of steepest descent optimization. For the validation of our adaptive design, we present the problem of Leukemia disease prediction. Simulations are presented to validate the performance of the proposed RBFNN kernel in contrast to the conventional RBFNN kernels.
Keywords
Radial basis function; Neural networks; RBF kernel; PDZ domain classification; Leukemia cancer prediction
Introduction
Broomhead and Lowe were the first to introduce the Radial basis function neural network (RBFNN). Its concept was based on the Cover’s Theorem [1,2]. The RBFFNN is known as universal approximate due to its remarkable performance in the problem of function approximation [3-5]. Originally, the RBF networks were designed for data interpolation in a higher dimensional space [5]. However, its applications are in wide area of engineering and it has been used as an important tool for function approximation, prediction, estimation, and system control [4-9]. The main advantage of RBF compared to other algorithms based on neural networks is the simplicity of computation of its network parameters [5]. The RBF networks perform the complex nonlinear mapping of the data that enables a fast, linear, and robust learning mechanism without significant computational cost [2].
Some of the most commonly used basis kernels are: Gaussian kernels [2], multi-quadric kernels [2], inverse multi-quadric functions [2], thin-plate spline kernels [5], and cosine kernels [10] etc. However, the selection of a proper kernel is highly problemspecific. A usual design of an RBFNN involves the learning of the centers of the kernels, the widths of the kernels, and weights of the networks [2]. In this context, a huge amount of work is carried out in the literature [11-16].
The most commonly used RBF kernel is the Gaussian kernel which employs the Euclidian distances between the feature vectors and the centers of the kernels [2]. However, it is shown in [10] that there can be scenarios where cosine distances are more significant in separating the features compared to the Euclidean. Thus, the work in [10] developed an RBF kernel by employing a linear combination of Gaussian kernel and cosine distance based kernel. Later, a time varying combination of the two kernels is proposed in [17] to improve the overall performance. In this work, a weighted cosine RBF kernel is proposed in which the conventional cosine distance is weighted by a diagonal matrix. We show that the weighting matrix can either be application dependent or it can be made adaptive via steepest descent based optimization. For the first case, we present two different applications: (1) PDZ domain classification and (2) Channel estimation for correlated inputs. For the second case, we develop a mechanism to recursively update the weighting matrix for the weighting matrix via steepest descent minimization of mean square error (MSE) cost function. This adaptive weighting matrix based RBF kernel is used for Leukemia disease prediction problem.
The main contributions of this study are as follows:
1) In Section (Proposed Weighted Cosine Rbfnn (Wc-Rbfnn)), we propose a novel weighted cosine RBF kernel where the weighting is introduced in: i) the inner product of input and neuron’s center, ii) norm of the input vector, and iii) norm of the center vector.
2) In Section (Choice of Weighting Matrix for the Wc- Rbfnn), we show how the weighting matrix can be chosen differently for different applications in order to optimize the performance of the WC-RBFNN. For that purpose, we present two examples: the PDZ domain classification and the channel estimation problem with correlated inputs.
3) In Section (Design of an Adaptive Weight for Wc-Rbfnn), we develop an automatic mechanism to update the weighting matrix for an arbitrary data using the approach of steepest descent optimization. For the validation of our adaptive design, we present the problem of Leukemia disease prediction.
The paper is organized as follows: Following this introduction, we provide an overview of the conventional RBF kernels in Section (Overview of the Conventional Rbf Kernels). In Section (Proposed Weighted Cosine Rbfnn (Wc-Rbfnn)), we develop the proposed weighted cosine RBF kernel. The choice of weighting matrix for the WC-RBFNN is discussed in Section (Choice of Weighting Matrix for the Wc-Rbfnn). In Section (Design of an Adaptive Weight for Wc-Rbfnn), an adaptive strategy is developed to make the weighting matrix of the WC-RBFNN time varying. Simulation results are presented in Section (Simulation Results). Finally, the concluding remarks are provided in Section (Conclusion).
Overview of the Conventional Rbf Kernels
In this section, we provide an overview of existing RBFNNs which are conventionally used in the literature. The RBFNN transform the nonlinear classification to linear classification by mapping the data into a higher dimensional space using some nonlinear kernel. According to Covers theorem, translation of features from lower dimension to a higher dimension simplifies the classification task via linear separation [1].
The RBFNN consists of three layers: an input layer, a hidden layer, and a linear output layer as shown in Figure 1. All inputs are connected to each hidden neuron. The input vector is passed through the hidden layer which consists of nonlinear mapping function. The ith neuron of the hidden layer employs a nonlinear kernel (denoted by 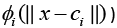 to compute distance between the input vector x and its center vector ci. The nonlinear kernels are of different types which can be categorized broadly into two: Euclidian Distance based and Cosine Distance based. These are discussed in the ensuing sub-sections.
to compute distance between the input vector x and its center vector ci. The nonlinear kernels are of different types which can be categorized broadly into two: Euclidian Distance based and Cosine Distance based. These are discussed in the ensuing sub-sections.
A. Euclidian distance based RBF kernels
Most commonly used RBF kernels are as follows [2],
Multiquadrics:
Most commonly used RBF kernels are as follows [2],
Multiquadrics: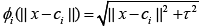 (1)
(1)
Inverse multiquadrics: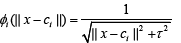 (2)
(2)
and Gaussian: 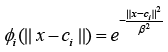 (3)
(3)
where Ƭ > 0, is a constant and β is spread parameter.
It can be seen from the above examples that the RBF kernels are usually function of the Euclidean distance between input and the center vectors. These distances are then mapped via some nonlinear functions such as Gaussian function given in (3). Here, the parameter β plays the role to adjust the sensitivity of the kernel. For example, its larger value will make the kernel less sensitive to a given input and vice versa.
B. Cosine distance based RBF kernels
One recent study [10] showed that there are scenarios where Euclidian distance becomes ineffective way of distinction. Thus, a cosine distance based RBF kernel was proposed in [10] which it evaluates the cosine distance between the input vector and the RBF’s center vector as follows:
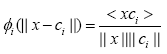 (4)
(4)
where < xci > is showing the dot product of vectors x and ci.
The term 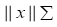 in (4) represents the weighted norm of the vector x which can be evaluated using the following definition:
in (4) represents the weighted norm of the vector x which can be evaluated using the following definition:
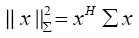 (5)
(5)
It is argued in [10] that the cosine distance based kernel is more suitable when the lengths of vectors are very close yet differ in their inclinations. Later this work was extended to a time varying convex combination of Euclidian distance based and cosine distance based kernels as follows [17]:
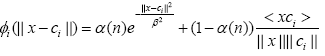 (6)
(6)
where α(n) is a time varying mixing parameter which is adapted by minimizing the mean square error cost function [17].
Proposed Weighted Cosine Rbfnn (Wc- Rbfnn)
In this study, we propose a weighted cosine RBF kernel in which weight to the dot product and to the norm of the individual vectors are provided which result in the following kernel:
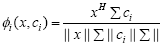 (7)
(7)
where Σ is a diagonal weight matrix with σm as its mth diagonal element, xHΣci is the weighted correlation between vectors x and ci such that:
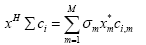 (8)
(8)
where M is the length of the vectors and xm and ci,m are the mth elements of x and ci, respectively.
The proposed RBF kernel given in (7) is named as Weighted Cosine RBF (WC-RBFNN).
**1The notation ()H denotes conjugate transposition operation. For the real input vectors, this is equivalent to taking transpose only [18].
Remarks
• The weighting matrix Σ is playing a role of giving specific importance to certain elements in the evaluation of cosine distance. In order to understand this further, we consider the weighted correlation between the two vectors x and ci defined in [8].
• It can be seen that the parameter σm is giving different weights to the mth term 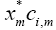 in this summation. Thus, if the correlation between x and ci is dominant due to certain terms, higher weights to these terms can increase their impact on the overall summation which eventually results in the enhancement of the cosine distance between the two vectors. Hence, the output of those neurons will be higher which are closer to specific input in terms of cosine distance.
in this summation. Thus, if the correlation between x and ci is dominant due to certain terms, higher weights to these terms can increase their impact on the overall summation which eventually results in the enhancement of the cosine distance between the two vectors. Hence, the output of those neurons will be higher which are closer to specific input in terms of cosine distance.
• Consider the two extreme scenarios:
a) If x = ci (showing full positive correlation), the WCRBFNN’s output for the ith neuron will be
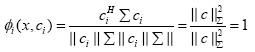 (9)
(9)
b) If x = -ci (showing full negative correlation), the WCRBFNN’s output for the ith neuron will be
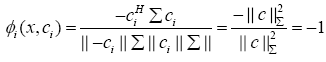 (10)
(10)
Thus, we conclude that the output of the WC-RBFNN’s neuron lies in the range [-1, +1] where extreme values show the full negative and full positive correlation cases, respectively.
Choice of Weighting Matrix for the Wc- Rbfnn
There can be an obvious question as how to choose the diagonal weighting matrix. This choice mainly depends on the application and which way the proposed RBF kernel is utilized. Some of the examples of specific applications are discussed in the following sub-sections.
A. Application in PDZ domain classification
PDZs are structural domains that are contained in numerous otherwise unrelated proteins. In general, they consist of approximately 90 amino acids and in the human genome are considered to be the most common protein domain [19]. PDZ domains are mainly recognized for their mediator role in the assembly of receptors at the cellular membrane interface [19-24]. Although, there are several PDZ domain classes; but, the two most dominant recognition patterns are X-S/T-S-φ for Class I PDZ domains and X-φ-X-φ for Class II PDZ domains [25,26]. There are many works in the field of protein and PDZ domain analysis. One of the recent work in [27], topological predictions for integral membrane transport proteins as well as guides for the development of more reliable topological prediction programs for family-specific characteristics are provided. In another work by [28], the response surface methodology (RMS) and artificial neural network (ANN) modeling were applied to optimize medium components for spinosad production. The Genetic Algorithm (GA) is used for ANN’s input optimization. They conclude that the hybrid ANN/GA approach provides a viable alternative to the conventional RSM approach for the modeling and optimization of fermentation processes. Related to protein study, another work in [29] provides molecular modelling of CtHtrA protein active site structure identified putative S1S3 sub site residues I242, I265, and V266.
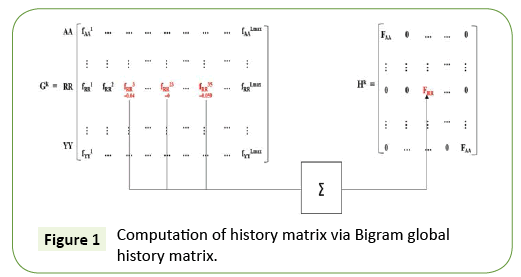
In our work, we focus on classifying the Class I PDZ domains (i.e., having X-S/T-S-φ pattern) and Class II PDZ domains (i.e., having X-φ-X-φ pattern) which were reported in [25,26] using a novel history weighted cosine RBF NN. Now, consider first the features we have used in our classification task. The set X = A, B, C, D, E, F, G, H, I, K, L, M, N, P, Q, R, S, T, V, W, Y is all possible amino acids (AAs). A protein sequence of length M, it has M-1 bigrams. For example, ABCDEFG has the following bigrams: AB, BC, CD, DE, EF, and FG. We computed the bigram normalized frequency of amino acids in a PDZ sequence by counting the number of times that bigram appears in the PDZ domain and dividing by M-1. To design the required weighting matrix Σ, we first evaluate the Bigram (Figure 1).
Global History Matrix (BGHM) denoted as Gk for the kth class. In order to compute BGHM, we first aligned our dataset separately for Class I and Class II PDZ domains using CLUSTALX 2.0 [30]. The concept of BGHM is illustrated in Figure 1, where we compute the global frequencies of every existing bigram for a set of PDZ domains sequences. Since, we are dealing with three classes of PDZ; therefore, we have three BGHMs: GI and GII. Every Column in Gk (k = I, II) indicates normalized frequencies of all possible bigrams at that position in every PDZ domain. To ease the computational burden, we set the number of columns in Gk to the length of the longest PDZ domain sequence for kth class. Once the BGHM for each class is evaluated, a history weight matrix (H) is computed as shown in Figure 2 for a given PDZ domain. To understand the computation of the history matrix H, consider the example of the PDZ domain ETRREIKLFKGPKGLGFSIAGGRRNQTKIIDGGA. In this PDZ sequence, the bigram ”RR” appears 3rd, 23rd, and 35th positions. Assuming that the corresponding elements in the BGHM Gk has entries 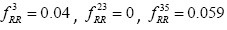 , respectively. Thus, the element in the history matrix H corresponding to the bigram RR is calculated by the summation of
, respectively. Thus, the element in the history matrix H corresponding to the bigram RR is calculated by the summation of 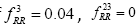
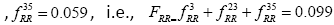 (as depicted by the Figure 1).
(as depicted by the Figure 1).
Finally, this history weight matrix H is used as the weighting matrix for the RBF, i.e., Σ=H and the resulting RBF is named as History weighted cosine RBFNN (HWC-RBFNN).
B. Application in channel estimation for correlated inputs
In this section, we show a a different domain of application for the proposed WC-RBFNN, that is, the channel estimation using the WC-RBFNN. Considering the problem of channel estimation in the presence of correlated inputs x. If the channel to be estimated is represented as an M×1 vector h, the output of the channel at iteration n can be expressed as o(n)=xHh+v(n), where v(n) is a zero mean i.i.d. noise sequence with variance σ2v and xi is M×1 zero mean correlated input vector with correlation matrix Rx, i.e., E[xxH] =Rx. The goal of the RBF is to estimate the unknown channel by minimizing the cost function
J(w)=E[e(n)2]
where e(n) is the estimation error given by;
e(n)=d(n)-y(n) (11)
where d(n) and y(n) are the desired response and the output of the RBF, respectively.
The desired response, in the case of channel estimation, is d(n)=o(n)=xHh+v(n) while the output of the RBF can expressed as y(n)=φT(x)w(n) The estimation of the channel is obtained via recursive computation of the RBF weights w(n) via steepest descent optimization as follows:
w(n+1)=w(n)+μe*(n)φT(x) (12)
It is known fact from the theory of adaptive filtering that the convergence speed of steepest descent optimization is severely degraded by the input correlation [18]. For example, if the adaptation is used by minimizing the mean-square-error cost function, the step-size μ is bounded as 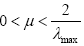 [18], where λmax is the maximum eigenvalue of the input correlation matrix Rx.
[18], where λmax is the maximum eigenvalue of the input correlation matrix Rx.
Thus, higher the correlation among the inputs, slower is the learning speed for the adaptation. The same can be true for the case of RBF based channel estimation. In order to deal with this issue, it is proposed to set the weighting matrix Σ as follows:
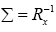 (13)
(13)
Knowing the fact that the input correlation matrix is Hermitian, we can factorize the Σ as2
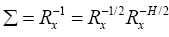 (14)
(14)
**2The representation RH/2 is a short notation for (R1/2)H.
By doing so, we can see that the output of the proposed RBF kernel for the ith neuron is transformed to
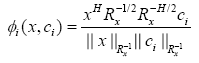 (15)
(15)
Now, if we define 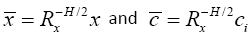 , we can write
, we can write 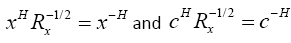
As a result, the above expression can be reformulated as:
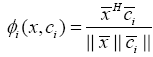 (16)
(16)
The correlation matrix of transformed vector 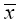 can be evaluated as:
can be evaluated as:
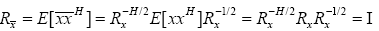 (17)
(17)
which proves that the input vector is transformed to a white vector with the choice of weighting matrix given in (14). Hence, the transformed output of the RBF given in (16) is now dealing with white input vectors which promise improvement in the convergence speed of the proposed RBFNN.
Design of an Adaptive Weight for Wc- Rbfnn
In this section, we aim to design the mechanism to make the weighting matrix Σ time varying. To do so, we employ the steepest descent approach to minimize the mean-squareserror (MSE) cost function, i.e., J(Σ)=e2(n), where e(n)=d(n)-y(n) is the error at the output for the nth iteration. We consider more general scenario in which every neuron has different weighting matrix. Thus, the steepest descent recursion for the weighting matrix of ith neuron is given by
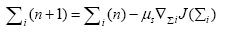 (18)
(18)
where 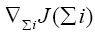 represents the gradient of cost function J(Σi) w.r.t to the weighting matrix Σi.
represents the gradient of cost function J(Σi) w.r.t to the weighting matrix Σi.
Since, Σi is a diagonal matrix such that diag 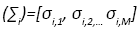 we can evaluate the
we can evaluate the 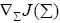 as
as
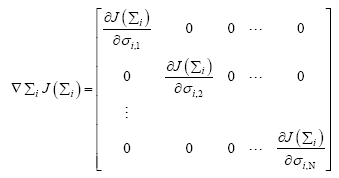 (19)
(19)
whose mth diagonal element can be evaluated as
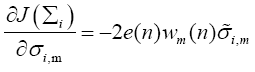 (20)
(20)
where wm(n) is the mth element in the weight vector w(n) and 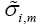 is defined as
is defined as
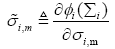 (21)
(21)
which is found to be
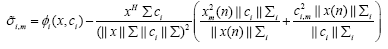 (22)
(22)
Thus, the adaptive weight matrix of the ith neuron can be computed via Equations (18), (19), (20), (21) and (22). Hence, the resulting WC-RBFNN utilizes an adaptive weighting matrix and it is abbreviated as AWC-RBFNN.
Simulation Results
In this section, we present three examples to investigate the performance of the two proposed variants of the WC-RBFNN in previous sections. These examples are discussed in detail in the ensuing subsections.
A. PDZ domain classification
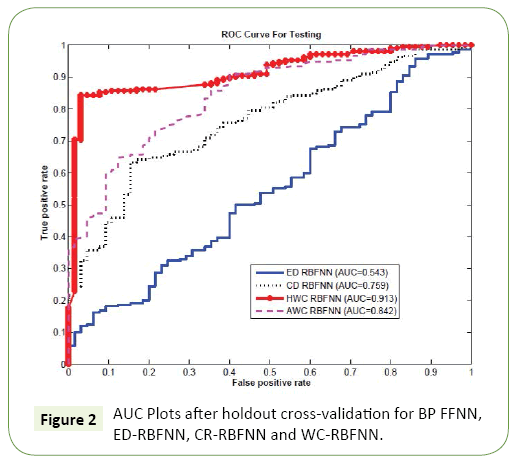
In order to validate the performance of our algorithm, we perform a comparative study using holdout cross validation and compare the performance of the proposed WC-RBFNN with the conventional variants of the RBFNN, that is, Eucledian Distance based RBF (ED-RBFNN), Cosine Distance based RBF (CDRBFNN). For the WC-RBFNN, we have used the two types of weighting matrix: One proposed in Section (Choice of Weighting Matrix for the Wc-Rbfnn- Application in PDZ Domain Classification), i.e., History Weighted WC-RBFNN or simply HWC-RBFNN and the other proposed in Section (Design of an Adaptive Weight for Wc-Rbfnn), i.e., AWC-RBFNN with adaptive weighting matrix. The data set of the PDZ domains we used are taken from the work in [25,26] which has two classes: Class I with 45 PDZ domains and Class II with 20 PDZ domains. This data set is divided into two sets: training and testing. In each run, we used training set to train the weights for NN and the testing set is used to evaluate the classifiers accuracy. Since Area Under Curve (AUC) is more discriminating measure than accuracy, we used AUC to compare the effectiveness of the two algorithms. Since our feature vectors are high dimensional the ED based classifier suffers with the challenge of dimensionality which is also evident in the ROC curve plots3 presented in Figure 2, that 3The ROC curves are the curves for true positive rate (TPR) vs false positive rate (FPR) shows the comparative ROC curve for the four RBF based classifiers: ED-RBF, CD-RBF, HWC-RBF, and AWC-RBF. The issue of dimensionality was so critical that the conventional ED-RBF could not manage it, yielding a poor AUC 0.543. The CD RBF performs better with AUC of 0.759. The AUC of 0.842 for the adaptive weighting based AWC-RBF shows its better performance compared to the ED-RBf and the CD-RBF. However, the HWC-RBF achieves the highest AUC of 0.913. This shows that the proper selection of weighting matrix can improve the overall performance and it can perform even better than the adaptive weighting matrix design (Figure 2).
**3The ROC curves are the curves for true positive rate (TPR) vs false positive rate (FPR).
B. Channel estimation in the presence of correlated inputs
Next, we investigate the proposed RBFNN for a channel estimation problem with an unknown channel selected as h=[0.227, 0.460, 0.688, 0.460, 0.227]T. The RBFNN used in this experiment has 10 numbers of neurons at the hidden layer. The input to the RBFNN and unknown channel is an M dimensional correlated complex Gaussian input which is generated with the following correlation matrix:
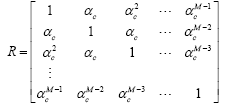
where 0 < αc < 1 is the factor that controls the correlation between the regressor elements.
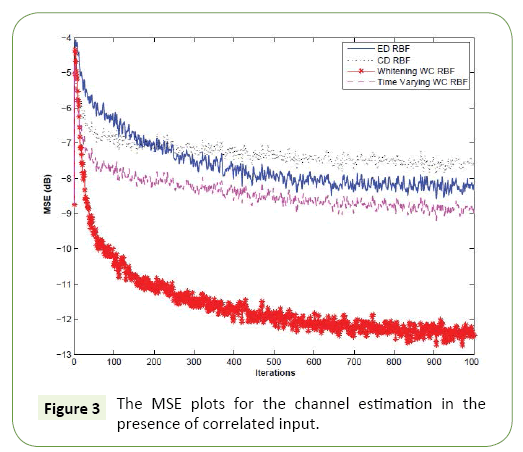
In this experiment, the input vector has the same length of that of the channel, that is, M=5. We set the SNR to 20 dB. We compare the MSE performance of the conventional ED-RBFNN, CD-RBFNN, the whitening based WC-RBFNN proposed in Section (Choice of Weighting Matrix for the Wc-Rbfnn- Application in Channel Estimation for Correlated Inputs) and the AWC-RBFNN proposed in Section (Design of an Adaptive Weight for Wc-Rbfnn) and the result is reported in Figure 3. It can be easily seen that the proposed whitening based WC-RBF out performed all of its counterparts in both convergence speed and the steady-state error. This indicates that the knowledge of weighting matrix for specific application can improve the performance and its performance is even better than that of the AWC-RBF.
C. Prediction of leukemia cancer
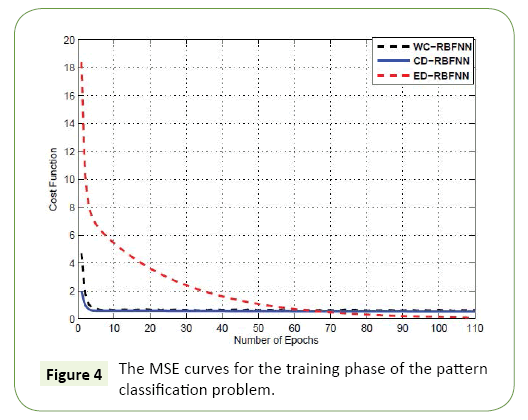
In this section, we present application from the field of bioinformatics, specifically, using gene microarray data as a tool to predict cancer. Using the standard Leukemia ALL/AML data [31], we aimed to develop a method of Leukemia prediction. The data set we used was comprised of both training and testing samples. More specifically, the bone marrow specimen consisted of 38 training samples (27 ALL and 11 AML) and 34 testing samples. These 34 test samples (20 ALL and 14 AML) are prepared using different experimental conditions and were isolated from either bone marrow (24) or by blood sample collection (10). In total, the dataset consisted of 7129 target genes. Minimum Redundancy and Maximum Relevance (mRMR) technique was used a way to isolate the most significant gene products, as it is well established in the field [32]. The mRMR approach yielded the top five genes for further experiments (Figure 3 and Table 1). For the training phase, the MSE curves of different approaches are shown in Figure 4.
Table 1 Results for the pattern classification problem.
Approach |
Training Accuracy | Testing Accuracy |
|---|---|---|
| Cosine kernel | 100.00% | 94.12% |
| Euclideankernel | 100.00% | 58.82% |
| WC-RBFNN | 100.00% | 97.06% |
The Euclidean kernel out performs the cosine kernel achieving a minimum MSE of 0.1033. The cosine kernel attained an MSE of 0.6934. The proposed method is able to undergo dynamic adaptation of the diagonal weighting matrix achieving an MSE of 0.5480. The Table 1 present the training accuracy of each of the cases studied. One important note is that in all cases, the training accuracy achieved is 100% for the training samples. However, a better evaluation for predictive systems is to look at the outcome of the testing stage, i.e., the unseen samples.
Even though, the Euclidean kernel initially achieved a high training accuracy in the training stage, its performance in the testing stage was relatively low at 58.82%. Therefore, the Euclidean kernel was likely over trained on the training samples and therefore incurred the problem of over fitting”. The kernel from this study using the proposed dynamic approach outperformed the both the conventional cosine and Euclidean kernels by a margin of 2.94% and 38.24%, respectively (Figure 4).
Conclusion
This work proposes a novel kernel for the Radial Basis Function Neural Networks (RBFNN). The proposed kernel is based on weighted cosine distance between the input vector and the center vectors associated with RBFNN. The weighting is introduced in:
i) the inner product of input and neuron’s center,
ii) norm of the input vector, and
iii) norm of the center vector.
We demonstrate how the weighting matrix can be chosen for different applications to optimize the performance of the WCRBF. As case studies, we present the PDZ domain classification and the channel estimation problem with correlated inputs. We also design an adaptive technique to update the weighting matrix for an arbitrary data using the approach of steepest descent optimization. For the validation of our adaptive design, we present the problem of Leukemia prediction. Simulations that were presented seem to validate the performance of the proposed RBFNN kernel in contrast to the conventional RBFNN kernels.
Acknowledgement
This project was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, under Grant No. (G/503/135/1436). The authors, therefore, acknowledge with thanks DSR for their technical and financial support.
References
- Cover TM (1965) Geometrical and Statistical properties of systems of linear inequalities with applications in pattern recognition. IEEE Transactions on Electronic Computers 14: 326-334.
- Haykin S (1994) Neural Networks: A comprehensive foundation.Pearson, Prentice Hall, PTR Upper Saddle River, NJ, USA.
- BroomheadDS, David Lowe (1988) Multivariable functional interpolation and adaptive networks.Complex Systems 2:21-355.
- Park J, Sandberg IW (1991) Universal approximation using radial-basis-function networks. Neural Computation 3:246-2257.
- Chen S, Cowan CFN, Grant PM (1991) Orthogonal least squares learning algorithm for radial basis function networks. IEEE Transactions on Neural Networks 2: 302-309.
- Kumar R, Ganguli R, Omkar SN (2010) Rotorcraft parameter estimation using radial basis function neural network. AppliedMathematics and Computation 216: 584-597.
- Savitha R, Suresh S,Sundararajan N, Kim HJ (2012) A fully complex-valued radial basis function classifier for real-valued classification problems. Neurocomputing 78: 104-110.
- Babu GS, Suresh S (2013) Sequential projection-based metacognitive learning in a radial basis function network for classification problems. IEEE Transactions on Neural Network and Learning Systems 24: 194-206.
- Oliveira OCD, Martins ADM, Araujo ADD (2017) Adual-mode control with a RBF network. J Control AutomElectrSyst 28: 180-188.
- Aftab W, Moinuddin M, Shaikh MS (2014) A novel kernel for RBF based neural networks. Abstract and AppliedAnalysis.
- Wettschereck D, Dietterich T (1992) Improving the performance of radial basis function networks by learning center locations. In Advances in Neural Information Processing Systems.
- Musavi MT, Ahmed W, Chan KH, Faris KB, Hummels DM (1992) On the training of radial basis function classifiers. Neural Networks 5: 595-603.
- Schwenker F, Kestler HA, Palm G (2001) Three learning phases for radial-basis-function networks.Neural Networks14: 439-458.
- Neruda R, Kudov P (2005) Learning methods for radial basis function networks. Future GeneratComputSyst 21: 1131-1142.
- Ali SSA, Moinuddin M, Raza K, Adil SH (2014) An adaptive learning rate for RBFNNusing time-domain feedbackanalysis. The Scientific World Journal.
- Raitoharju J, Kiranyaz S, Gabbouj M (2016) Training radial basis function neural networks for classification via class-specific clustering. IEEE Transactions on Neural Network and Learning Systems 27: 2458-2471.
- Khan S, Naseem I, Togneri R, Bennamoun M (2017) A novel adaptive kernel for the RBF neural networks. Circuits,Systems, and Signal Processing 36: 1639-1653.
- Sayed AH (2003)Fundamentals of adaptive filtering. Wiley-Interscience, New York.
- Tsunoda S, Sierralta J, Sun Y, Bodner R, Suzuki E, et al. (1997) A multivalent PDZ-domainprotein assembles signalling complexes in a G-protein-coupled cascade. Nature 388:243-249.
- Fanning AS, Anderson JM (1999) PDZ domains: Fundamental building blocks in the organization of protein complexesat the plasma membrane. J Clin Invest 103:767-772.
- Harris BZ, Lim WA (2001) Mechanism and role of PDZ domains in signalling complex assembly.J Cell Sci114:3219-3231.
- Doyle DA,Lee A, Lewis J, Kim E, Sheng M, et al.(2001) Crystal structures of a complexed and peptide-freemembrane protein-binding domain: molecular basis of peptide recognition by PDZ. Cell 85:1067-1076.
- Sheng M, Sala C (2001) PDZ domains and the organization of supramolecular complexes. Annu RevNeurosci 24: 1-29.
- Songyang Z, Fanning AS, Fu C, Xu J, Marfatia SM, et al. (1997) Recognition of unique carboxyl-terminal motifs by distinct PDZ domains. Science 275:73-77.
- Wiedemann U, Boisguerin P, Leben R, Leitner D, Krause G, et al. (2004) Quantificationof PDZ domain specificity, prediction of ligand affinity and rational design of super-binding peptides. J MolBiol343:703-718.
- Kalyoncu S, Keskin O, Gursoy A (2010) Interaction prediction and classification of PDZ domains.BMC Bioinformatics11:357.
- Reddy A, Cho J, Ling S, Reddy V, Shlykov M, et al.(2014) Reliability of nine programs of topological predictions and their application to integral membrane channel and carrier proteins. J MolMicrobiolBiotechnol24:161-190.
- Lan Z, Zhao C, Guo W, Guan X, Zhang X (2015) Optimization of Culture Medium for Maximal Production of Spinosad Usingan Artificial Neural Network-Genetic Algorithm Modeling. J MolMicrobiolBiotechnol 25:253-261.
- Gloeckl S, Tyndall JDA, Stansfield SH, Timms P, Huston WM (2012) Theactive site residue V266 of chlamydial HtrAis critical for substrate binding during both in vitro and in vivo conditions. J MolMicrobiolBiotechnol22:10-16.
- Larkin MA, Blackshields G, Brown N, Chenna R, McGettigan PA, et al. (2007) Clustal W and Clustal X version 2.0. Bioinformatics 23:2947-2948.
- Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, et al.(1999) Molecular classification of cancer: Class discovery and class prediction by gene expression monitoring. Science 286: 531-537.
- Peng H, Long F, Ding C (2005) Feature selection based on mutual information criteria of max-dependency, max-relevance, andmin-redundancy. IEEE Transactions on Pattern Analysis and Machine Intelligence 27: 1226-1238.
Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences