Keywords

Perihelion precession; Artificial earth satellite; Spaceflight; Aerospace; Modification of gravity; General relativity; Astrophysics; Astronomy

Description

Astronomical observations found that Mercury's orbit around the sun revolve against the clock, and the orbit is not closed, this is the precession of Mercury. The precession of Mercury's perihelion calculated by Newton's law of universal gravitation is not consistent with the observed value. In 1859, the French astronomer Urbain Le Verrier found that the observed value of the perihelion precession of Mercury was 38" per century faster than the theoretical value calculated by Newton's laws, and speculated that this might be caused by the attraction of a planet closer to the sun than Mercury. But after years of painstaking searching for the suspected planet, there was no sign of it. The American astronomer, Newcomb, S., calculated that Mercury's anomalous precession rate was 43"/century, and later put forward some theories to explain Mercury's anomalous precession, but none of them succeeded. So, Newcomb suspects that the law of square inversion in the law of gravity is problematic. For the purpose of explaining the actual motion of several inner planets at the same time, Newcomb worked out that the gravitational force should be inversely proportional to 2.1574 power of the distance. At the end of the 19th century, Weber, Riemann and others, at the early stage of the development of electromagnetic theory, tried to explain the precession of Mercury's perihelion with electromagnetic theory, but they failed to get satisfactory results.

In 1916, Einstein published his famous general theory of relativity, declaring success in explaining the precession of Mercury's perihelion. General relativity calculates the displacement pre- cation value of 0.43 " annually by a linear approximation and suggests that the Mercury precession generation is due to spacetime bending.

In the paper “The Physical Cause of Planetary Perihelion Precession", the author gives another explanation for mercury's perihelion precession. The author thinks that the reason for mercury's perihelion precession is that the closer the planet is to the sun, the more it deviates from (or exceeds) the value calculated by Newton's universal gravitation formula [1]. If this is true for Mercury's perihelion precession, then we can conclude that artificial Earth satellites will also produce precession at the perigee.

To prove that artificial Earth satellites produce precession at perigee by using the modified universal gravitation formula

For an artificial earth satellite with a gravitational mass of m, according to the modified universal gravitation formula (2.9), the magnitude of the universal gravitation experienced by the artificial Earth satellite is:

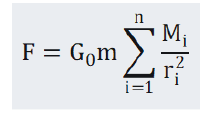
In formula (2.1), G0 is a constant, Mi  is the gravitational mass of any celestial body in the universe, ri is the distance between the center of mass of the artificial earth satellite and the center of mass of the celestial body with gravitational mass of Mi, and the sum sign is the sum of all celestial bodies in the universe [2]. Since the earth is the closest massive celestial body to the satellite, in order to simplify the calculation, we only retain the earth term in the sum term on the right side of Equation (2.1), and discard all other terms，and replace G0 with the gravitational constant G:

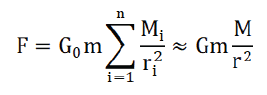
In the above equation, M is the gravitational mass of the earth, and r is the distance between the center of mass of the satellite and the center of mass of the earth. Because the earth is close to the satellite and can’t be regarded as a particle, in order to improve the accuracy of the calculation, we divide the earth into n small pieces. According to the revised law of gravity, the gravity between the satellite and the earth is:

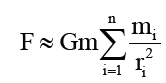
In the above equation, mi is the gravitational mass of any small piece after the earth is divided into n small pieces [2].

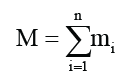
r_i is the distance between the center of mass of the satellite and the center of mass of the small piece with gravitational mass of mi, and the sum sign is the sum of all the n small pieces that divide the earth. Since the gravitational mass of the earth can be regarded as a continuous distribution, the sum of Equation (2.3) can be changed to an integral:

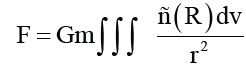
In the above formula, ρ(R) is the gravitational mass density distribution of the earth, and v is the volume of the earth. When the satellite is far from the earth and can treat the earth as a particle, we have:

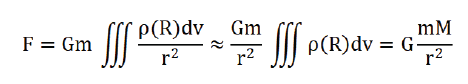
where, mI is the inertial mass of the satellite. In this case, the gravitation of the satellite is in good agreement with Newton's universal gravitation formula and the motion of the satellite is in good agreement with Newton's motion equation. When the satellite is close to the earth and the earth can’t be regarded as a particle, we have:

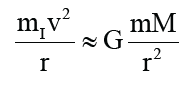
In this case, the gravity of the satellite deviates from Newton's gravitational formula, the motion of the satellite deviates from Newton's equation of motion, and the closer the satellite is to the earth, the greater the deviation.

Calculation of the perigee precession of artificial earth satellites

The artificial earth satellite orbits the earth according to the following formula:

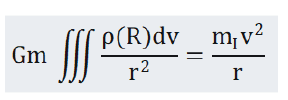
Where, G is gravitational constant, m is gravitational mass of artificial earth satellite, mI is inertial mass of artificial Earth satellite, and ρ(R) is gravitational mass density distribution of the Earth. If the gravitational mass is equal to the inertial mass, then:

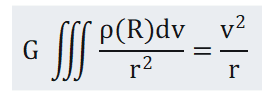
Considering the influence of earth aether wind, Formula (3.2) should be modified as

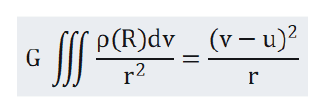
In Formula (3.3), u is the velocity of the earth's aether wind relative to the Earth, v is the velocity of the satellite relative to the Earth, and v-u is the velocity of the satellite relative to the Earth's aether wind. Using formula (3.3), the computer should accurately simulate the motion of the artificial Earth satellite and calculate the precession of the artificial Earth satellite [3,4].

Conclusion

The simulation results for the ground-based microsatellite telemetry transmission is discussed here which follows three steps in sequence: telemetry data generation, raw data with binary CCD's images collection, and the usage of PBP protocol for transmission. First of all, a software is developed to generate the forty channel data to simulate the artificial satellite's system telemetry and health report in which the basic data format resembles a group of PACSAT satellites all artificial earth satellites operating in an elliptical orbit produce precession at perigees. Second, the CCD's images and the re-coded raw data are collected and stored afterwards for further transmission. Third, through the PBP protocol, the data are broadcasted to another ground station. In such a test, the data communication loop is completed. It is hoped that the global scientific community, especially the space scientific community, will verify this conclusion.

References

1. Wang, J.A. (2021) The Physical Cause of Planetary Perihelion Precession. Research Square.
2. Wang, J.A. (2021) The Modification of Newton's Gravitational Law and its Application in the Study of Dark Matter and Black Hole. Research Square.
3. Wang, J.A. (2020) On the dynamics of ocean currents and atmospheric circulation (is it possible for viruses to spread along latitude lines through atmospheric circulation?.
4. Wang, J.A. (2020) Mpemba Effect- the Effect of Time?. Science open