Keywords

Light trapping; Turnip moth; Night sky polarization

Introduction and Literature Background

Verkhovskaya [1] described the first time that the arthropods (Arthropoda) are able to distinguish between the polarized light and not polarized light. She stated that many diurnal animals are able to perceive linearly polarized light.

The theory of polarization of skylight has a long history. The single scattering Rayleigh-method [2] describes the majority of the skylight polarization quite well, although there are areas (especially around the neutral points), where there are substantial differences between the Rayleigh-theory and the reality [3]. Berry [4] suggested a method to overcome the weaknesses of the Rayleigh-method which describes the polarization pattern of the whole clear sky quite accurately.

The polarization pattern of the sky in various sky conditions is nowadays well known thanks to the spread of full-sky imaging polarimeters. The degree of polarization is maximal along a great circle of the sky being 90 degree from the Sun, and minimal at the Sun and anti-Sun as well as at the Arago, Babinet and Brewster neutral points [5]. The degree of polarization also depends on the atmospheric conditions. In cloudy and foggy skies, as well as under canopies the degree of polarisation are much smaller compared to clear skies [6-8]. However, the direction of polarization pattern is very robust, even under forest canopies, where light scattering occur only in a very thin air layer under the foliage, the typical 8-shaped pattern as well as the axis of symmetry is well recognizable. The axis of symmetry of the direction of polarization pattern is the celestial great circle containing the Sun and anti-Sun during the daylight [5]. When the Sun is well below the Horizon and the Moon lights the atmosphere, then the axis of symmetry is the celestial great circle containing the Moon and anti-Moon [9]. Barta et al. [10] inspected the transition of characteristics of sky polarization between sunlit and moonlit skies during twilight.

According to Sotthibandhu and Baker [11] in case of a moonlit night the Moon azimuth is used as a signal as an information for orientation. In starlit night when the Moon is absence the stellar orientation about 95° from the pole star to strongly concerned [11].

Dacke et al. [12] wrote many animals are able to use the solar polarization pattern of the sky for their orientation, but the Scarabeus zambesianus Péringuey, 1901 is the first insect, who is able to use for this purpose in the moonlight million-fold less than the brightness of the solar polarization.

Dacke et al. [13] wrote the beetles remain more active in moonlit nights than the moonless nights, possibly using the Moon as a source for their guidance when it comes to polarized light patterns are no longer available.

These important new findings are confirmed in subsequent studies. They show the relative role of the moon in orientation. They conclude that the moon is not a primary tool for orientation. The effective cue polarization pattern around the moon is more reliable for orientation [14].

Dacke and Horváth [15] and Dacke et al. [16] found that the Bogong Moths (Agrotis infusa Boisduval, 1832) can use several types of celestial compasses that run along straight tracks. These are the Sun, the Moon, the Polarized Light Pattern, and even the Milky Way, which is far more prominent than a single star.

Dacke et al. [16] suggest that manure bugs are the only animal species that are known to be using a lot of faint polarization patterns around the Moon as compasses to maintain the road.

However, the Moon is not visible every night and the intensity of the sky polarization pattern taper off as the Moon disappears. It is extremely important to state of Dacke et al. [16] that celestial orientation is as precise during First and Last Quarters of Moon as it is during Full Moon. Moreover, this orientation precision is equal to that measured for diurnal species that orient under the 100 million times brighter polarization pattern formed around the Sun. This indicates that, in nocturnal species, the sensitivity of the optical polarization compass can be greatly increased without any loss of precision [16].

However, the Moon is not visible every night, and the intensity of the sky polarization will cease as the Moon disappears. Extremely important is that orientation is just as accurate during the First and Last Quarters of the Moon under the Full Moon. In addition, this orientation accuracy is the same as that of the daily species based on a polarization pattern of 100 million times around the Sun. This suggests that the sensitivity of the optical polarization compass may increase considerably in the light of the night, without being imprecise [16].

Kyba et al. [17] found that in the bright moonlit nights in a highly polarized light bands stretching from the sky at 90 degrees to the Moon, and has recently shown that the nocturnal organisms are able to navigate it.

Several authors found that the polarized light-traps collect more insects than the unpolarized ones [18-22].

Dacke et al. [16] found that the celestial orientation is as precise during First- and Last Quarters of Moon as it is during Full Moon.

This fact suggests that the insects are able to use polarized moonlight for spatial orientation. Therefore they fly in higher amount the First- and Last Quarter to light than other lunar phases.

Several authors reported about it:

Nowinszky et al. [21]: Coleoptera: Serica brunnea L., Melolontha melolontha L., Lepidoptera: Operoptera brumata L., Hyphantria cunea Drury, Agrotis segetum Den. et Schiff.),

Danthanarayana and Dashper [22] Certain mosquitoes and moths,

Nowinszky et al., [23,24] Operophtera brumata L. and eight Trichoptera species,

Nowinszky and Puskás [25-28] twenty-four Microlepidoptera species; Lygus sp.; Ostrinia nubilalis Hbn.

Nowinszky et al. [28] seven Microlepidoptera species caught by pheromone traps.

Material

Járfás [29] constructed and operated a fractionating lighttrap (next hour collecting killing jar) in Hungary (Kecskemét- Katonatelep, geographical coordinates are: 46°54′53″N and 19°41′57″E) between 1967 and 1969, during three years. This light-trap gave a priceless substance with a scientific value for the entomology researches.

This light-trap worked from 1^st April to 31^st October, from 7 p.m. to 5 a.m. every night of the year, regardless of weather, or the time of sunrise and sunset.

The light source of Járfás type fractionating light-trap composed of 3 pieces of 120 cm long F-33 type 40W light tubes placed above each other.

We worked up the collecting data of Turnip Moth (Agrotis segetum Denis et Schiffermüller, 1775) in connection with the data of 41 environmental factors.

The data of weather elements as follow: air temperature (°C), precipitation (mm), wind speed (km/h), air pressure (hPa), relative humidity (%) and cloud cover (okta=eight part) values were got from the Year-Books of Hungarian National Weather Service.

The Q-index data, which were processed in this study, were calculated by T. Ataç and A. Özgüç from Bogazici University Kandilli Observatory, Istanbul, Turkey. Its calculation is made by the following formula: Q=(i x t) where i=flare intensity, t=the time length of its existence.

Geomagnetic field strength can be divided into three divisions: H=horizontal, Z=vertical and D=declination components. The distance of 300 km along the geomagnetic meridian does not yet have significantly different properties. Thus, geomagnetic data recorded in Hungary at a single observation site provides relevant information across the country. These measurements were made at the observatory of the Geophysical Institute of Eötvös Loránd University of Tihany. The H-index values were used above 2150 nT [30].

Methods

The astronomical data were calculated with a program based on the algorithms and routines of the VSOP87D planetary theory for Solar System ephemeris and written in C by J Kovács. The additional formatting of data tables and some further calculations were carried out using standard Unix and Linux math and text manipulating commands. For computing the tidal potential generated by the Sun and the Moon we used the expansion of the gravitational potential in Legendre polynomials and expressed the relevant terms as a function of horizontal coordinates of the celestial objects.

We calculated the degree of polarization of clear sky lit by the Sun and by the Moon separately at the Zenith for every half hour between 1^st January 1967 and 31^st December 1969. For this we first determined the celestial position of the Sun and the Moon for every point in time of the above interval for a geographic position of 46° 54' 26.64"N and 19° 41' 30.12"E (Kecskemét, Hungary) [31] with the atmospheric refraction taken into account. We then calculated the degree of polarization of the clear sky at the Zenith by using the Berry-method [4]. For this calculation we assumed a neutral point distance of 27.5° and for the sake of simplicity a maximum of degree of polarization of 100%. Note, that during this paper we did not use the absolute degree of polarization, instead only their relative ratios, so assuming 100% maximum degree of polarization does not influence our end results, despite being a non-real scenario.

Using our own computer program, we investigated the lighting data required for the tests. György Tóth, an astronomer, developed this program on the TI 59 computer we used in our joint research [31]. This program was adapted to a modern computer by Miklós Kiss, associate professor.

The program calculates the light for any geographic location, day and time day, or twilight and night, separately and altogether, from Sun, Moon and starlight. Clouds are also taken into account in its calculation [32]. The clouds data were provided by the Annals of the Hungarian Meteorological Service. In these books, the data are recorded every 3 hours in octa [33].

The values of ambient illumination (lux) and moonlight (lux) were calculated using this program.

The collection distance was calculated from the light intensity of the lamp (candle) and the ambient illumination (lux) using the following formula:

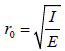
Where: r_o=the collecting distance, I=the intensity of illumination by the light-trap (candela), E=the intensity of environmental illumination (lux).

The values of colour temperature of moonlight were calculated by our own computer programme for a former study [34] by the following formula:

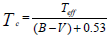
Where T_c=Colour temperature of Moon, T_eff=Colour temperature of Sun=5850 °K, (B-V)=Colour index of Moon depending on the phase angle of Moon.

The connection with colour index and the absolute value of Moon’ phase angle:

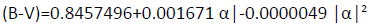
We have calculated the relative catch values of the number of caught moths by broods. Basic data were the number of individuals caught by one night. In order to compare the differing sampling data of species, relative catching values were calculated from the number of individuals. For the examined species the relative catch (RC) data were calculated for each sampling night per year. The RC was defined as the quotient of the number of specimen caught during a sampling time unit (1 night) per the average catch (number of specimen) within the same generation relating to the same time unit. For example when the actual catch was equal to the average individual number captured in the same generation/swarming, the RC value was 1 [33].

The relative catch data were classified into the appropriate phase angle groups. The phase angle groups and the corresponding catch data were organized into classes. Their number was determined according to Sturges' method [34] using the following formula:

k=1+3.3 * 1gn

Where: k=the number of divisions, n=the number of observation data.

The time of New Moon, First Quarter, Full Moon and Last Quarter were taken from homepage of U.S. Naval Observatory Astronomical Applications Department.

The other phase angle divisions were calculated from these.

We have divided the 360° phase angle of the full lunar month (lunation) into 30 divisions. All divisions include 12 phase angle values. The phase angle division in vicinity of a New Moon contains phase angles 354°-360° and 0°-6° and named 0. Starting from here, divisions in the direction of the First Quarter until the Full Moon were named: 1 (6°-18°), 2 (18°-30°), 3 (30°-42°, 4 (42°- 54°), 5 (54°-66°), 6 (66°-78°, 7 (78°-90°, 8 (90°-102°), 9 (102°-114°), 10 (114°-126°), 11 (126°-138°), 12 (138°-150°), 13 (150°-162°), 14 (162°-174°). The division including the Full Moon was named: 15 (174°-186°). Also starting from the Full Moon, divisions in the direction of the Last Quarter until a New Moon were named: -1 (186°-198°), -2 (198°-210°), -3 (210°-222°), -4 (222°-234°), -5 (234°-246°), -6 (246°-258°), -7 (258°-270°), -8 (270°-282°), -9 (282°-294°), -10 (294°-306°), -11 (306°-318°), -12 (318°-330°), -13 (330°-342°), and -14 (342°-354°). We have arranged all nights of the observation period into one of these phase angle divisions.

The data thus obtained are tabulated. We determined that the expected value (1) in which Moon Quarter is significantly divergent from the relative catch value. Because in the First and Last Quarter was found high-value relative catch we were looking relationship with the polarized moonlight values.

Cluster and factor methods were used with the use of SPSS 19 software package.

Our goal was to explain the relative catch (RC) variance as best as possible by reducing the number of other 41 variables.

The first approach was taken together with all of the 41 variables. The data for the Sun and Moon were calculated with this program as list those (abbreviations in parentheses).

Azimuth angle of Sun (Sun-Az), Altitude of Sun above horizon (Sun-Alt), Zenith distance of Sun (Sun-ZD), Gravitational potential of Sun (Sun-Pot), Azimuth angle of Sun Arago point (Sun-Ar-Az), Altitude os Sun Arago point above horizon (Sun-Ar-Alt), Azimuth of Sun Babinet point (Sun-Ba-Az), Altitude of Sun Babinet point above horizon (Sun-Ba-Alt), Azimuth odf Sun Brewster point (Sun- Br-Az), Altitude of Sun Brewster point above horizon (Sun-Br-Alt), Sky polarization originated from Sun (Sun-Sky-Pol), Gravitational potential of Sun and Moon (Sun-Moon-Pot), Azimuth of Moon (Moon-Az), Altitude of Moon above horizon (Moon-Alt), Zenith distance of Moon (Moon-ZD), Apparent magnitude of Moon (Moon-Vmagn), Illuminated fraction of Moon (Moon-Phase), Gravitational potential of Moon (Moon-Pot), Moonlight (Moon- Lux), Azimuth of Moon Arago point (Moon-Ar-Az), Altitude of Moon Arago point above horizon (Moon-Ar-Alt), Azimuth of Moon Babinet point Moon-Ba-Az), Altitude of Moon Babinet point above horizon (Moon-Ba-Alt), Azimuth of Moon Brewster point (Moon-Br-Az), Altitude of Moon Brewster point above horizon (Moon-Br-Alt), Sky polarization originated from Moon (Moon-Sky-Pol).

We calculated azimuth values from North to East-South-West direction.

Additional environmental factors were

Phase angle divisions of Moon (°), Polarized moonlight (%), Environmental illumination (lux), Collecting distance (metres), Air temperature (°C), Wind speed (km/h), Relative humidity of air (%), Clouds (okta), Air pressue (hPa), Colour temperature (°K), Hours of collecting nights, Q-index (Features of solar activity), Height of Tropopause (km) and H-index (Horizontal component of geomagnetic field).

By performing cluster analyzes, we continuously filtered out the most influential factors for catch. We have determined the factors which are the most important for the effectiveness of the catch. We depicted these and also the results coming from the different factors and the connection with catch. Since our catch data have Poisson distribution, the spreads are roughly the same as averages. Figures also show the confidence intervals.

Results and Discussion

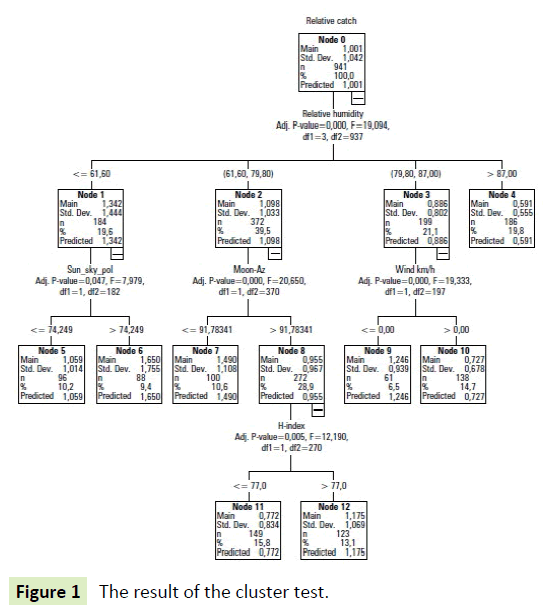
The results of cluster test are shown in Figure 1. There can be seen in the tree structure the Humidity (on level 1), Sun-Sky-Pol, Moon-Az, Wind (on level 2) and H-index (on level 3). It can be stated that Humidity is one of the predominant variables (the factor weight is the largest), which lists the RC values into 4 intervals.

The most important factors were the sky polarization generated by the Moon and the Sun and the relative humidity of the air. If the relative humidity of the air was lower than 61.60 % the effect of Sun-Sky-Pol occurs. Presumably, smaller vapours have no influence on the degree of polarization of the sky and the structure of the polarization planes (arrangement of 8 or lemniscate), so the insect can use polarization and the structure of the polarization planes for orientation. Based on the Sun-Sky- Pol values, the RC values are divided into two groups. If Sun-Sky- Pol is >74.249, then RC=1.650, otherwise RC=1.059. That is, the Sun’s sky polarization will result in a greater relative catch. The role of humidity can be explained by the fact that, in the case of high humidity, the polarization pattern in the sky is distorted.

If the humidity reaches the medium value (61.60-79.80 %) this is determining variable together with Moon-Sky-Pol, Moon-Pol and Clock factors. The additional analyses confirmed this fact. The Moon-Sky-Pol especially prevails if Moon-Az value is <=91.78341. From the collection hours (2 to 6), the Moon polarity from the Moon is greater than the Sun's polarity, so Moon's effect prevails.

Here RC=1.490 in the collection hours is permanently bigger, than RC=1.

The results of the cluster analysis were confirmed and complemented by our individual calculations based on each factor.

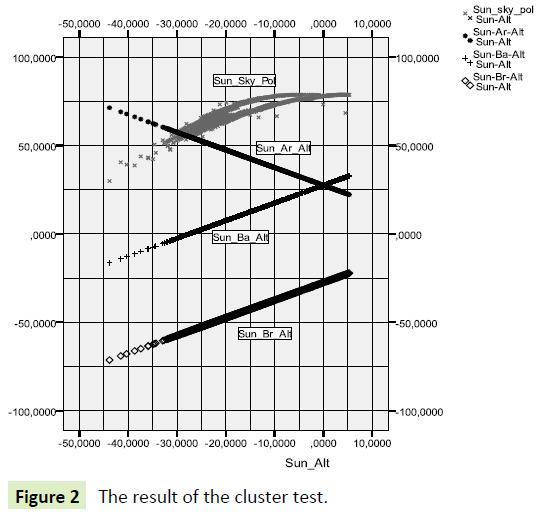
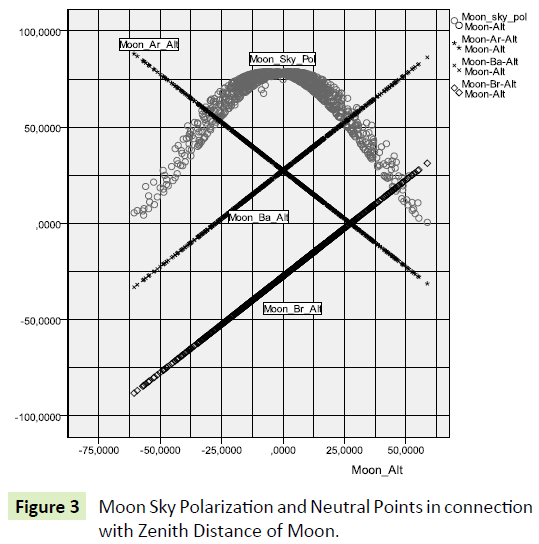
Figures 2 and 3 illustrate the position of the neutral points above the horizon as a function of the distance between the Sun and the Moon.

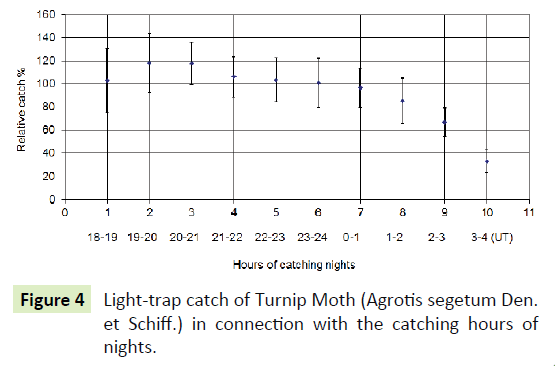
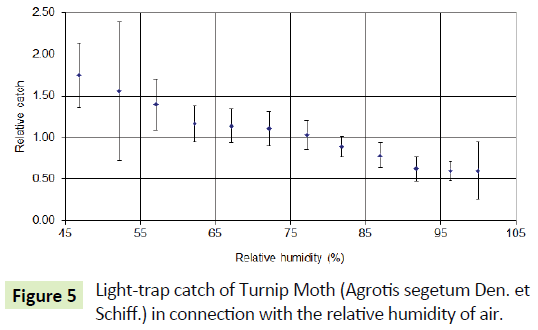
The catch decreases during the hours of the night collection and in addition to the circadian rhythm of species, the rising relative humidity from evening to dawn as well as decreasing air temperature affects it (Figures 4 and 5).

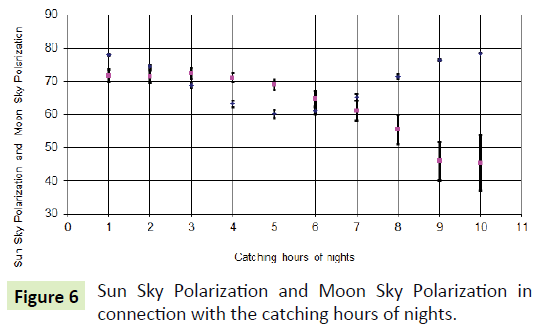
The Sun-Sky-Polarization and Moon-Sky-Polarization can be seen in connection with the catching hours of nights in Figure 6.

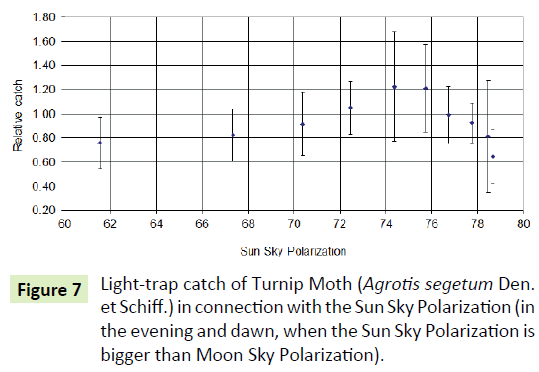
The catch of Turnip Moth was increase in the evening and dawn, when the Sun-Sky-Polarization is bigger than Moon-Sky- Polarization.

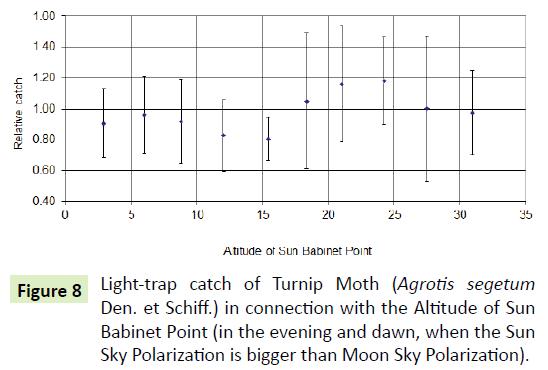
The catch of Turnip Moth was increase in the evening and dawn, when the Sun-Sky-Polarization is bigger than Moon-Sky- Polarization. The catch is reduced on the highest value, but this situation only can be seen when the Sun is just above the horizon, or it is directly below the horizon. The Sun Babinet point change together with the distance of the Sun above horizon, but the Sun Arago point changes in the opposite direction. The catch changes according to this fact (Figures 7 and 8).

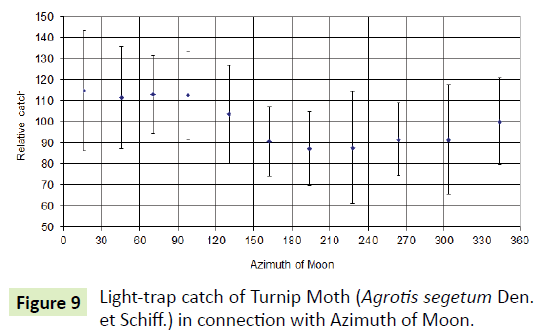
The azimuth angle of the moon also strongly influences the effectiveness of the catch. When the Azimuth is <91.7, the Moon is slightly above or below the horizon. In this case, the moon phase is in the neighbourhood of the last quarter, the polarities of the moonlight are highest. The Moon polarization (Moon-Sky- Pol) generated by the Moon is high and the relative catch (RC) is also high. The RC values can be further divided into two groups according to the H-index values. If H index is>77.0 then RC=1.176, otherwise RC=0.772. The horizontal component of the Earth's magnetic field has a little effect on the relative catch (Figure 9).

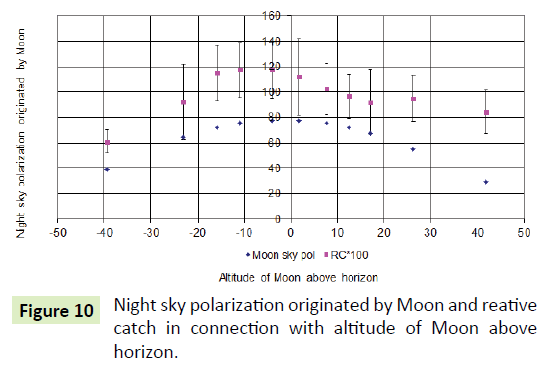
The altitude of the Moon above horizon and the sky polarization generated by the Moon are in a strong connection with each other (Figure 10).

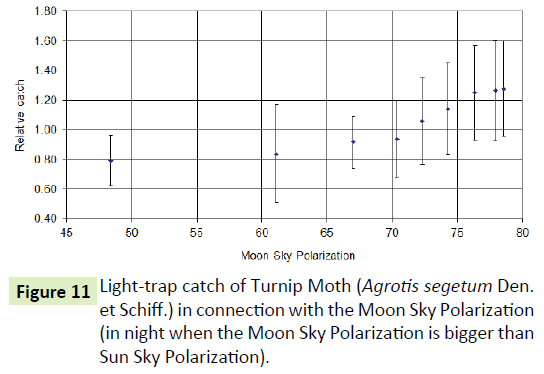
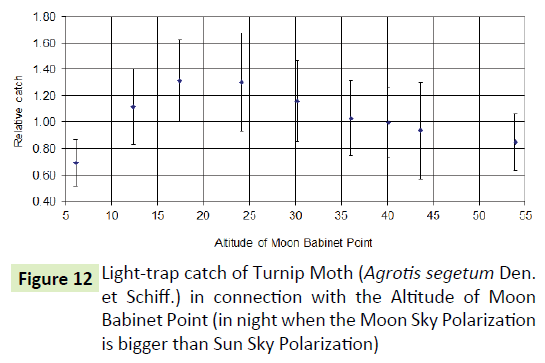
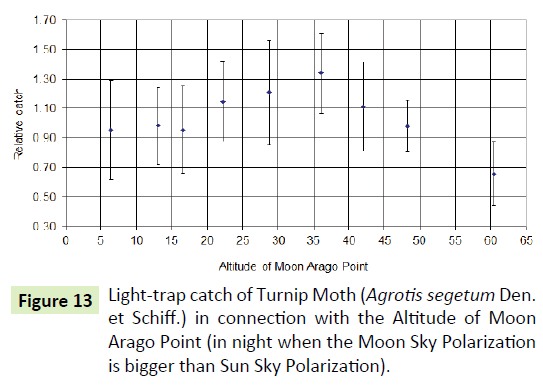
The catch is most effective when the Moon is in the vicinity of the horizon. At this time is the highest Moon-Sky-Pol, and at this time there is the highest catch belonging to Moon's Arago and Moon's Babinet points (Figures 11-13).

The Moon-Sky-Pol has the most important effect for catch, because the RC almost completely follows this influence. In contrast, both the Arago and the Babinet points may only play a role in the near moon horizon, neither before nor after, there is not a clear correlation between the two neutral points’ situation above the horizon and the RC.

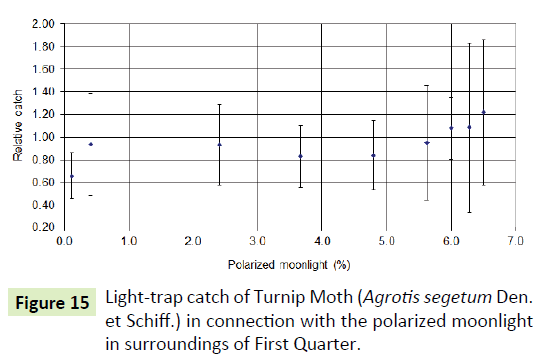
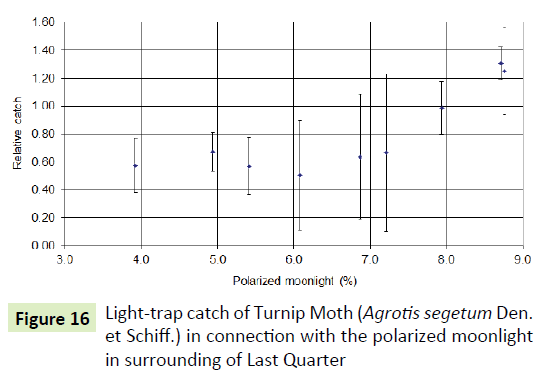
If Moon-Az is>91.78341, then the Moon-Pol, the polarity of the moonlight also influences the catch, which has its effects in the first and last quarters. There is a smaller effect in the first lunar quarter, but in the last quarter a bigger local maximum can be experienced. These peaks are caused by the polarized moonlight, which is higher in the last quarter.

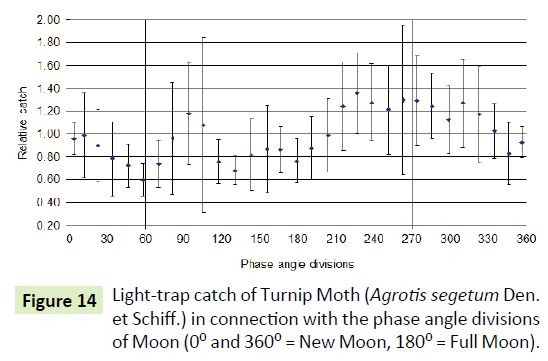
Moon-Pol can be depicted as a function of the phase angle; the Moon-Az is in a contact with the phase angle. If the structure of 8 of the polarisation planes is created then its slow rotation may indicate the passing of time for the insect around the zenith (Figures 14-16).

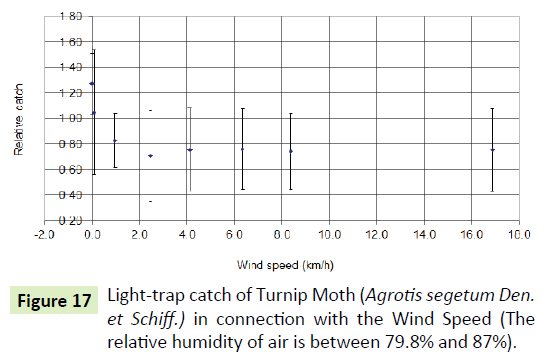
In the case of higher humidity (79.80-87.00), the degree and order of the polarity does not prevail, or it is less prevalent. Otherwise, at dawn there is more humidity, less catch, and the role of the H-index and/or wind variables may increase. When the wind is calm the RC is bigger, because RC=1.246, anyway RC=0.727 (Figure 17).

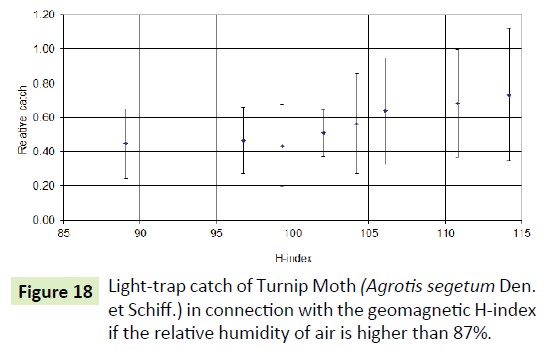
In case of very high humidity (above 87%), the sky polarization pattern may be less presumably used by the insect. That is why the catch increases with the increase in the value of the H-index.

The effect of the factors that we did not detail only modifies the catch to a little bit, so we don’t deal with these in this study. We could not demonstrate a significant relationship with the colour temperature of the moonlight, and we will report the gravitation of the Sun and the Moon in a separate study though with the significant influence (Figure 18).

Naturally, our results refer only to the turnip moth (Agrotis segetum Denis et Schiffermüller), but it is assumed that other insect species have similar effects.

For this reason, it would be important to use fractionated traps as many collections as possible for further research (light traps, pheromone traps, suction traps, etc.).

Acknowledgements

Flare Index Data used in this study were calculated by T. Ataç and A. Özgüç from Bogazici University Kandilli Observatory, Istanbul, Turkey. The Q-index daily data for the period 1967 and 1969 were provided by Dr. T Ataç. His help is here gratefully acknowledged.

We also would like to thank J Kovács (ELTE Astrophysical Observatory, Szombathely) for calculating the Moon and Sun data and describing the method of investigation.

References

1. Verkhovskaya IN (1940) The influence of polarized light upon the phototaxis of certain organisms. Bulletin of Moscow society and Naturlist. History of Social Biological Section 49: 101-113.
2. Coulson KL (1988) Polarization and intensity of light in the atmosphere. Deepak, Hampton.
3. Suhai B, Horváth G (2004) How well does the Rayleigh model describe the E-vector distribution of skylight in clear and cloudy conditions? A full-sky polarimetric study. Journal of the Optical Society of America 21: 1669-1676.
4. Berry MV, Dennis MR, Lee RL (2004) Polarization singularities in the clear sky. New Journal Physcis 6: 162.
5. Horváth G, Gál J, Pomozi I, Wehner R (1998) Polarization portrait of the Arago point: Video-polarimetric imaging of the neutral points of skylight polarization. Naturwissenschaften 85: 333-339
6. Horváth G, Barta A, Gál J (2002) Ground-based full-sky imaging polarimetry of rapidly changing skies and its use for polarimetric cloud detection. Applied Optics 41: 543-559.
7. Hegedüs R, Åkesson S, Wehner R (2007a) Could Vikings have navigated under foggy and cloudy conditions by skylight polarization? On the atmospheric optical prerequisites of polarimetric Viking navigation under foggy and cloudy skies. Proceedings of the Royal Society A 463: 1081-1095.
8. Hegedüs R, Barta A, Bernáth B (2007b) Imaging polarimetry of forest canopies: how the azimuth direction of the sun, occluded by vegetation, can be assessed from the polarization pattern of the sunlit foliage. Applied Optics 46: 6019-6032.
9. Gál J, Horváth G, Barta A (2001) Polarization of the moonlit clear night sky measured by full-sky imaging polarimetry at full moon: Comparison of the polarization of moonlit and sunlit skies. Journal of Geophysical Research D (Atmospheres) 106: 22647-22653.
10. Barta A, Farkas A, Száz D (2014) Polarization transition between sunlit and moonlit skies with possible implications for animal orientation and Viking navigation: anomalous celestial twilight polarization at partial moon. Applied Optics 53: 5193-5204.
11. Baker RR, Sotthibandhu S (1979) Celestial Orientation by the Large Yellow Underwing Moth, Noctua pronuba L. Animal Behaviour 27: 786-800.
12. Dacke M, Nilsson DE, Scholtz CH (2003a) Insect orientation to polarized moonlight. International weekely journal of science 424: 33.
13. Dacke M, Byrne MJ, Scholtz CH (2003b) Lunar orientation in a beetle. Proceeding of the royal society of London 271: 361-365.
14. Dacke M, Baird E, Byrne M (2013) Dung beetles use the Milky Way for orientation. Current Biology 23: 1-3.
15. Dacke M, Horváth G (2014) Polarized Light Orientation in Ball-Rolling Dung Beetles, Polarized Light and Polarization Vision in Animal Sciences, Springer Series in Vision Research, pp: 27-39.
16. Dacke M, Byrne MJ, Baird E (2011) How dim is dim? Precision of the celestial compass in moonlight and sunlight. Philosophical translation of the royal society 366: 697-702.
17. Kyba CCM, Ruhtz T, Fischer J (2011) Lunar skylight polarization signal polluted by urban lighting. Journal of Geophysical Research 116: D24106.
18. Kovrov BG, Monchadsky AS (1963) The possibility of using polarized light to attract insects. Entomological Review 42: 25-28.
19. Szentkirályi F, Bernáth B, Kádár F (2003) Flight of ground beetles towards polarized and unpolarized light sources. European Carabidology 114: 313-324.
20. Meltser N, Kash Y, Broza M (2008) Does polarized light guide Chironomids to navigate toward water surface. Biol Mus Mun Funchal Sup 13: 141-149.
21. Nowinszky L, Szabó S, Tóth GY (1979) The effect of the moon phases and of the intensity of polarized moonlight on the light-trap catches. Z ang Ent 88: 337-355.
22. Danthanarayana W, Dashper S (1986) Response of Some Night-Flying Insects to Polarized Light. Insect Flight pp: 120-127.
23. Nowinszky L, Hirka A, Csóka GY (2012a) The influence of polarized moonlight and collecting distance on the catches of winter moth Operophthera brumata L. (Lepidoptera: Geometridae) by light-traps. European Journal of Entomology 109: 29-34.
24. Nowinszky L, Kiss O, Szentkirályi F (2012b) Influence of illumination and polarized moonlight on light-trap catch of caddisflies (Trichoptera). Research Journal of Biology 2: 79-90.
25. Nowinszky L, Puskás J (2013) Light-trap catch of harmful Microlepidoptera species in connection with polarized moonlight and collecting distance. Journal of Advanced Laboratory Research in Biology 4: 108-117.
26. Nowinszky L, Puskás J (2014) Light-trap catch of Lygus species (Heteroptera: Miridae) in connection with the polarized moonlight, the collecting distance and the staying of the Moon above horizon. Journal of Advanced Laboratory Research in Biology 5: 102-107.
27. Nowinszky L, Puskás J (2015) Light-trap Catch of European Corn-borer (Ostrinia nubilalis Hübner) in Connection with the Polarized Moonlight and Geomagnetic H-Index. Annual of Natural Sciences 1: 3-8.
28. Nowinszky L, Puskás J, Barczikay G (2015) The Relationship between Polarized Moonlight and the Number of Pest Microlepidoptera Specimens Caught in Pheromone Traps. Journal of Polish Entomology 84: 163-176.
29. Járfás J (1979) Forecasting of harmful moths by light-traps.
30. Nowinszky L, Puskás J (2011) Light trapping of the turnip moth (Agrotis segetum Den. et Schiff.) depending on the geomagnetism and moon phases. Applied Ecology and Environmental Research 9: 303-309.
31. Nowinszky L, Tóth GY (1987) Influence of cosmic factors on the light-trap catches of harmful insects. PhD Dissertation Keszthely (in Hungarian).
32. Nowinszky L, Puskás J (2017) Light-Trap Catch of Insects in Connection with Environmental Factors, Biological Control of Pest and Vector Insects, Agricultural and Biological Sciences.
33. Nowinszky L (2003) The Handbook of Light Trapping. Savaria University Press Szombathely pp: 272.
34. Odor P, Iglói L (1987) An Introduction to the Sport’s Biometry. ÁISH Tudományos Tanácsának Kiadása, Budapest, pp: 267.