ISSN : 2393-8854
Global Journal of Research and Review
Common Fixed Point Theorem in Sequentially Complete Hausdorff Ordered Uniform Spaces
Department of Mathematics, Saffrony Institute of Technology, Linch, Mehsana, India
Abstract
In this paper we obtain coincidence point and common fixed point theorem for contraction type mappings satisfying a contractive inequality using generalized altering distance function in ordered uniform spaces. In this paper I considering sequentially complete Hausdorff ordered Uniform space, four sequentially continuous mappings and their pairs are compatible and two mappings are increasing with respect to other two. Keywords: Ordered uniform space, Coincident point, Common fixed point, Compatible pair of mappings, Altering distance function, Generalized weakly C-contraction.
Keywords
Ordered uniform space, Coincident point, Common fixed point, Compatible pair of mappings, Altering distance function, Generalized weakly C-contraction.
Introduction
The well known Banach fixed point theorem for contraction mapping has been generalized and extended in many directions. Since the uniform spaces form a natural extension of the metric spaces, there exists a considerable literature of fixed point theory dealing with results on fixed or common fixed points in uniform spaces.
A new category of fixed point problems was addressed by Khan et al [12].They introduced the notion of an altering distance function which is a control function that alters distance between two points in a metric space.
Definition 1.1 [12]
The function 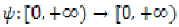 is
called an altering distance function, if the
following properties are satisfied:
is
called an altering distance function, if the
following properties are satisfied:
(i) 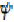 is continuous and non decreasing,
is continuous and non decreasing,
(ii) 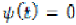 if and only if
if and only if 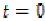 .
.
Altering distance has been used in metric fixed point theory in recent papers [3,6,11,14]. Choudhury [2] also introduced the following definition.
Definition 1.2 [2]
A 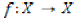 mapping , where
mapping , where 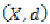 is a metric space is said to be weakly Ccontractive
if for all
is a metric space is said to be weakly Ccontractive
if for all 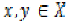 , the following
inequality holds:
, the following
inequality holds:
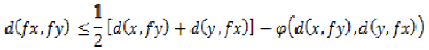
Where 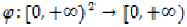 is a
continuous function such that
is a
continuous function such that 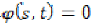 if
and only if
if
and only if 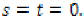
In [2] the author proves that if X is complete then every weak C- contraction has a unique fixed Point. Also fixed point theorems in partially ordered spaces and sequentially complete Hausdorff ordered uniform spaces are given in [1,4,5,7,9,13].
In this paper we establish some coincidence and common fixed point results for four self mappings on a Hausdorff sequentially complete ordered uniform spaces satisfying a generalized weak Ccontractive condition which involves altering distance function.
Now, we recall some relevant definitions and properties.
We call a (X, U) pair to be a
uniform space which consists of a non
empty set X together with a uniformity U. It
is well known (see Dugundji [8] and Kelley [10]
that any uniform structure U on X is induced
by a family D of pseudometrics on X and
conversely any family D of pseudometrics
on a set X induces on X a structure of
uniform space U. In addition, U is Hausdorff
if and only if D is separating. A family 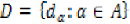 of pseudometrics on X is said
to be separating if for each pair of points
of pseudometrics on X is said
to be separating if for each pair of points 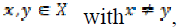 there is a
there is a 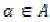 such
that
such
that 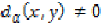 .
.
Consider a uniform space (X, U) with
a uniformity U induced by a family 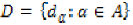 of pseudometrics on X. A
sequence
of pseudometrics on X. A
sequence 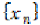 of elements in X is said to be
Cauchy if for every
of elements in X is said to be
Cauchy if for every 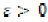 and
and 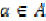 , there is
an N with
, there is
an N with 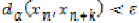 for all
for all 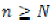 and
and 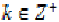 . The sequence
. The sequence 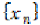 is called
convergent if there exists an
is called
convergent if there exists an 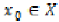 such for
every
such for
every 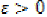 and
and 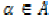 , there is an N with
, there is an N with 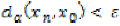 for all
for all 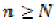 . A uniform space is called sequentially complete if any
Cauchy sequence is convergent. A subset of
X is said to be sequentially closed if it
contains the limit of any convergent
sequence of its elements.
. A uniform space is called sequentially complete if any
Cauchy sequence is convergent. A subset of
X is said to be sequentially closed if it
contains the limit of any convergent
sequence of its elements.
Let X be a non-empty set, 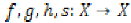 are given self mappings on X.
If
are given self mappings on X.
If 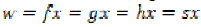 for some
for some 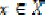 , then x is called a coincidence point of
, then x is called a coincidence point of 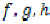 and s, and w is called a point of coincidence of
and s, and w is called a point of coincidence of 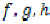 and s. If
and s. If 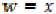 , then x is called a
common fixed point of
, then x is called a
common fixed point of 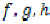 and s.
and s.
Definition 1.3 [7]
Let 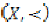 be a partially ordered set.
Two mappings are said to be weakly
increasing if
be a partially ordered set.
Two mappings are said to be weakly
increasing if 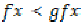 and
and 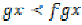 for all
for all 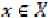 .
.
Let X be a non-empty set and 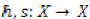 be a given mapping. For every
be a given mapping. For every 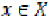 , we denote by
, we denote by 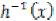 and
and 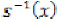 the
subset of X defined by:
the
subset of X defined by:
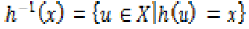
And 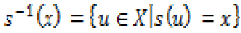
Definition 1.4
Let 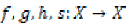 are given self
mappings on X. The pair
are given self
mappings on X. The pair 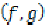 is said to be
compatible if
is said to be
compatible if 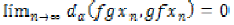 for
each
for
each 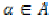 , whenever
, whenever 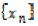 is a sequence in X
such that
is a sequence in X
such that 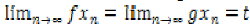 for some
for some 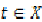 .
.
MAIN RESULT
Theorem 2.1
Let 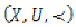 be a sequentially
complete Hausdorff ordered uniform space.
Let
be a sequentially
complete Hausdorff ordered uniform space.
Let 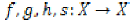 be given mapping
satisfying.
be given mapping
satisfying.
(i) 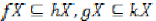 ,
,
(ii) 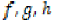 and
and 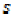 are sequentially
continuous,
are sequentially
continuous,
(iii) the pairs 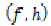 and
and 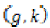 are
compatible,
are
compatible,
(iv) 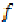 and
and 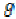 are weakly increasing with
respect to
are weakly increasing with
respect to 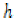 and
and 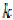 .
.
Suppose that for every 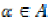 and
and 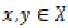 such that
such that 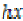 and
and 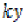 are comparable,
we have.
are comparable,
we have.
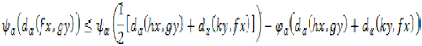
Where for each 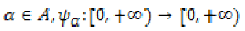 is an altering
distance function and
is an altering
distance function and 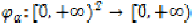 is a continuous function with
is a continuous function with 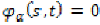 if
and only if
if
and only if 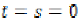 .
.
Then 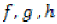 and
and 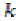 have a coincidence
point
have a coincidence
point 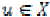 , that is,
, that is, 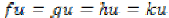 .
.
Proof
Let 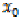 be an arbitrary point in
be an arbitrary point in 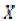 . Since
. Since 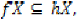 there exists
there exists 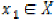 such that
such that 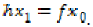 Since
Since 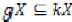 , there exists
, there exists 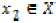 such that
such that 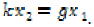 Continuing this process,
we can construct sequences
Continuing this process,
we can construct sequences 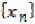 and
and 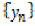 in
X defined by.
in
X defined by.
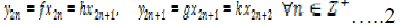
By construction, we have 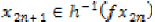 and
and 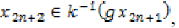 then using the fact that f and g are weakly
increasing with respect to h and k, we
obtain.
then using the fact that f and g are weakly
increasing with respect to h and k, we
obtain.
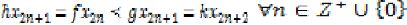
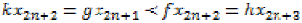 Then
Then 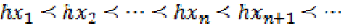 Or
Or 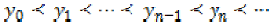
Since 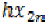 and
and 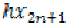 are
comparable for each
are
comparable for each 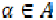 by inequality (1),
we have.
by inequality (1),
we have.
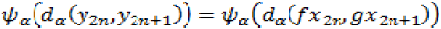
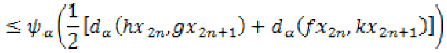
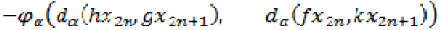
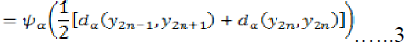
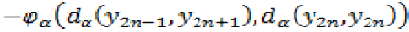
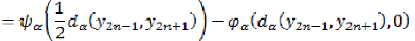
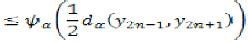
Since 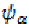 is a non decreasing function,
we get that.
is a non decreasing function,
we get that.
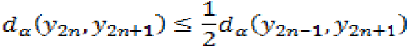
By triangular inequality, we have.
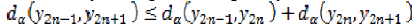 …………………………..4 Thus
…………………………..4 Thus
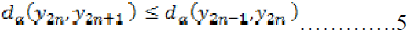
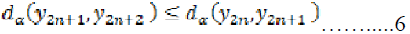
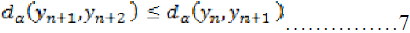
It follows that the sequence 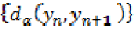 is monotonic decreasing.
Hence, there exists
is monotonic decreasing.
Hence, there exists 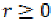 such that.
such that.
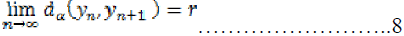
By (4) we have
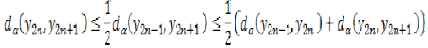 …………………………………….………9
…………………………………….………9
Taking  and using (8), we get-
and using (8), we get-
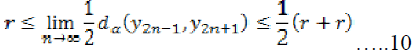
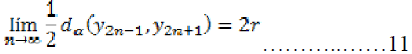
Taking 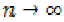 in (3) and using the
continuity of
in (3) and using the
continuity of 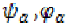 and (8), (11) we get
that-
and (8), (11) we get
that-
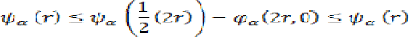
Which implies that 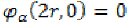 and
hence
and
hence 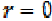 , so we have.
, so we have.
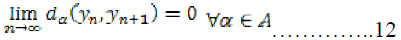
To prove that 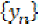 is a Cauchy
sequence in X, it is sufficient to show that
is a Cauchy
sequence in X, it is sufficient to show that 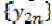 is a Cauchy sequence. Suppose to the contrary, that
is a Cauchy sequence. Suppose to the contrary, that 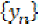 is not a Cauchy sequence.
Then there exists
is not a Cauchy sequence.
Then there exists 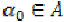 and
and 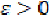 for which
we can find two subsequences
for which
we can find two subsequences 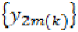 and
and 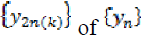 such that
such that 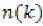 is the smallest
index for which,
is the smallest
index for which,
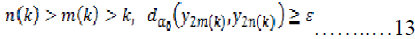
This means that,
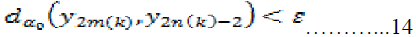
Therefore, we use (13), (14) and triangular inequality to get,
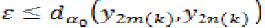
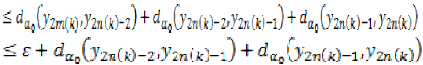
Taking 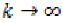 in the above inequality
and using (12), we find,
in the above inequality
and using (12), we find,
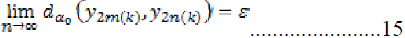
On the other hand, we have,
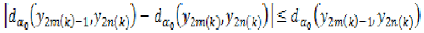
Taking  in the above inequality
and using (12), (15) we find,
in the above inequality
and using (12), (15) we find,
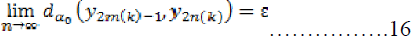
On the other hand, we have,
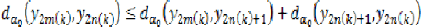
Taking 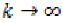 in the above inequality
and using (12), (15) we have,
in the above inequality
and using (12), (15) we have,
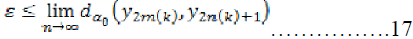
Also, by triangular inequality, we have,
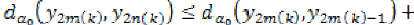
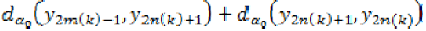
Taking again 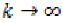 in the above
inequality and using (12), (15) and (16) we
find,
in the above
inequality and using (12), (15) and (16) we
find,
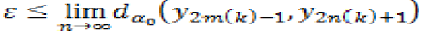
Similarly, we can show that,
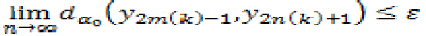
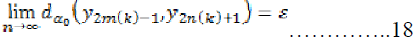
From (1), we have,
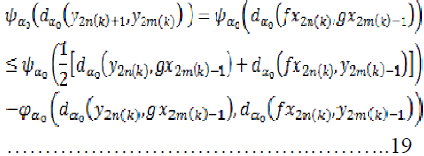
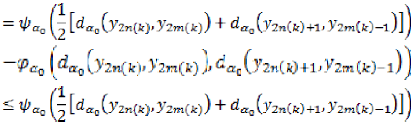
Since 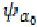 is a non decreasing
function, we get that,
is a non decreasing
function, we get that,
Taking again  in the above
inequality and using (15), (18) we find,
in the above
inequality and using (15), (18) we find,
Therefore, from (17) and (20) we have,
Taking 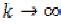 in (19) and using (15),
(18), (21) and the continuity of we find
in (19) and using (15),
(18), (21) and the continuity of we find 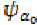 and
and 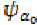 , we get that,
, we get that,
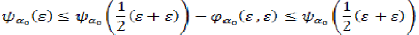
Which implies that 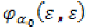 and
hence =0, a contradiction. Thus
and
hence =0, a contradiction. Thus 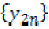 is a
Cauchy sequence and hence
is a
Cauchy sequence and hence 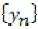 is a Cauchy
sequence. Since
is a Cauchy
sequence. Since 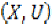 sequentially complete
Hausdorff uniform space, there is
sequentially complete
Hausdorff uniform space, there is 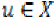 such
that,
such
that,
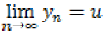
Therefore,
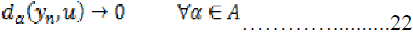
From the sequentially continuity of h and k, we get,
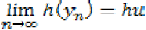
Therefore,
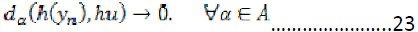
The triangular inequality and (2) yields,
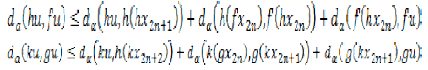
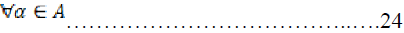
From (2) and (22),
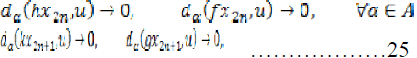
The pair 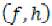
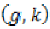 is
compatible, then,
is
compatible, then,
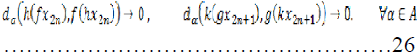
Using the sequentially continuity of 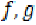 and (25), we have,
and (25), we have,
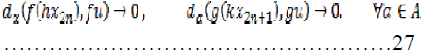
Combining (23), (26) together with
(27) and taking 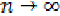 in (24), we obtain,
in (24), we obtain, 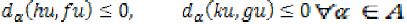
Which means that 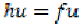 and
and 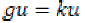 . So u is a coincidence point of
. So u is a coincidence point of 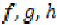 and
and 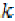 .
.
REFERENCES
- A. Amini-Harandi and H. Emami, 2010. A fixed point theorem for contraction type maps in partially ordered metric spaces application to ordinary differential equations. Nonlinear Anal., 72: 2238-2242.
- B.S. Choudhury, 2009. Unique fixed point theorem for weak C- contractive mappings. Kathmandu Univ. J. Sci. Eng. Tech., 5(1): 6- 13.
- G.V.R. Babu, B. Lalitha and M.L. Sandhya, 2007. Common fixed point theorems involving two generalized altering distance functions in four variables. Proc. Jangeon Math. Soc., 10: 83-93.
- H. Ayadi, 2011. Coincidence and common fixed point result for contraction type maps in partially ordered metric spaces. Int. J. Math. Anal., 5(13): 631-642.
- H. Ayadi, H.K. Nashine, B. Samet and H. Yazidi, 2011. Coincidence and common fixed point results in partially ordered cone metric spaces and applications to integral equations. Nonlinear Anal., 74: 6814-6825.
- H.K. Nashine, B. Samet, 2011. Fixed point results for mappings satisfying - weakly contractive condition in partially ordered metric spaces. Nonlinear Anal., 74: 2201-2209.
- I. Altun and H. Simsek, 2010. Some fixed point theorems on ordered metric spaces and applications. Fixed point theory and applications, 2010 Article ID 621469: 17 pages.
- J. Dugundji, 1966. Topology. Allyn and Bacon, Massachusetts USA.
- J. Esmaily, S.M. Vaezpour, 2012. Coincidence and common fixed point results for generalized weakly C-contraction in ordered uniform spaces. J. Basic. Appl. Sci. Res., 2(4): 4139-4148.
- J.L. Kelly, 1955. General topology. Van Nostrand Princeton, New York.
- K.P.R. Sastry and G.V.R. Babu, 1999. Some fixed point theorems by altering distances between the points. Indian J. Pure Appl. Math., 30: 641-647.
- M.S. Khan, M. Swaleh and S. Sessa, 1984. Fixed point theorems by altering distances between the points. Bull. Austral. Math. Soc., 30(1): 1-9.
- R.P. Agrawal, M.A. El-Gebeily and D. O’Regan, 2008. Generalized contractions in partially ordered metric spaces. Appl. Anal., 87:109-116.
- S.V.R. Naidu, 2003. Some fixed point theorems in metric spaces by altering distances, Czechoslovak Math. J., 53: 205- 212.
Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences
