Keywords
Voice multiplexing system; Overflow probability; Idle probability; Stochastic Fluid Model (SFM)
Introduction
With the development of the Internet, real-time voice transmission, such as Tencent meetings and DingTalk, has become an important part of people's real life. In such a packet voice switching system based on Asynchronous Transfer Mode (ATM), the packet voice signals are packaged into fixed-size voice packets and transmitted using a store-and-forward method. Telephone technology usually requires a bandwidth of more than 64 k bit/s, while the bandwidth required for the packet voice is usually less than 10 k bit/s, so packet voice technology is widely used in data communication systems and computer network systems. In the communication system, multiplexing technology combines multiple signals on a physical channel for transmission, which greatly improves the utilization of communication lines, and also saves the costs of the cable installation and maintenance.
Multiple voice sources share a link through the multiplexer in the form of statistical multiplexing. The voice source generates voice data stream and enters a multiplexing buffer, it is necessary for the packet signal to wait in the buffer for the processing of the system, thus the configuration of the system affects the quality of service (QoS) of the system, such as the call delay, speech intelligibility and so on.
The capacity of the multiplexing buffer is one of the important parts of the voice multiplexing system design [1]. Due to the randomness of the communication, the burst-scale queue phenomenon is always occurred in the voice multiplexing system [2], and this phenomenon is mainly related to the multiplexing buffer of the system. More specifically, if the buffer capacity is too large, it will affect the transmission delay of the voice stream and increase the cost of the system; if the buffer capacity is too small, the voice stream overflow possibility will increase, which will result in the problems such as the loss of voice information, the poor voice quality and so on. Obviously, the size of buffer makes an important impact on the QoS of voice transmission.
Starting from the pioneering work [3] of Anick, Mitra and Sondi in 1982, the Stochastic Fluid Model (SFM) has been widely used in various research fields. The stochastic fluid model can be defined as an input and output system, that is, SFM is modeled as a continuous fluid change process that enters and leaves the storage device (i.e. buffer) at a random changing rate. Anick et al. gave a stationary analytical solution of the SFM system [3]. In 2008, the authors of [4] analyzed the voice multiplexing system based on the Markov Modulated Poisson Process (MMPP) model, and estimated the broadband demand on the multiplexing node. In 2010, [5] proposed two independent finite state birth-death processes to study the occupancy distribution of the infinite capacity buffer, and gave a steady-state occupancy distribution of the buffer. In 2013, [6] calculated the steady-state probability when the buffer is empty based on the M/PH/1 fluid queue of the infinite buffer. In 2015, [7] combined the traditional fluid model and the fluid model based on Markov-renewal method to study the voice traffic queue phenomenon in the packet voice multiplexing system, and proposed a new method to calculation the mean buffer Occupancy. The literature [5-8] studied various performances of packet voice multiplexing systems by SFM modeling.
The main solution of the SFM system in the above literature is based on the spectral decomposition method [3-5]. This method gives a stationary analytical solution of the SFM system in an exponential form of the eigenvalue. However, the numerical calculation of this method is unstable when the eigenvalue is close to zero. Moreover, in practical applications, there may be a large number of system states in the system model, which will lead to various calculation difficulties and numerical algorithm problems [9]. On the other hand, in order to derive the performance metrics (such as overflow probability, etc.) of the system, this system is often approximated by the system model with the infinite capacity [6,7]. Obviously, this assumption is not unrealistic in practical problems, and this system model limits the accuracy of the performance in the practical application scenarios [8].
Motivated by these facts, in this paper, we analyze the packet voice multiplexing system based on the theoretical framework of the SFM. Compared to the literature mentioned above, and the main contributions of this paper are as follows:
• This paper proposes finite capacity SFM to describe the packet voice multiplexing system, That is, instead of infinite buffer, the multiplexing buffer in the packet voice multiplexing system is directly set to a finite capacity, when the voice traffic entering the buffer is larger than the capacity of the buffer, voice stream overflow will be occurred. Obviously, the finite capacity buffer is more suitable for practical application scenarios, and the obtained analysis performance is more accurate.
• To analyze the packet voice multiplexing system under the finite capacity SFM framework, we use the method introduced in [10] in this paper. Firstly, the system path is truncated, and then based on which, Matrix-Analytic Methodology is used to derive the exact expressions of the overflow and idle probabilities. This method has stronger stability and faster convergence speed than spectral decomposition method. Based on the above performance metrics, we investigate the characteristics of overflow and idle probabilities of the buffer, we also discusses the parameter setting in packet voice multiplexing system, that is, the size of the buffer and the number of users that can be accommodated are analyzed numerically.
Model and Problem Formulation
Throughout this paper, we use the following notations. For a matrix A, denote its (i,j) -th element by Aij and let Aij be the block matrix of A. Assume that 0, I and 1 represent zero matrix, unit matrix and unit vector with an appropriate dimension, respectively.
Subsection
Similar to literature [4,9] we consider a packet voice multiplexing system as shown in Figure 1. There are N mutually independent voice sources, which are indexed by 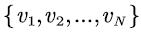 . Each voice source has two states: active (that is, voice call phase) and silent (that is, voice pause), and each voice source alternates between the two states. The voice stream generated by each voice source in the active period enters the data buffer at a constant rate. We assume that the capacity, which is denoted by
. Each voice source has two states: active (that is, voice call phase) and silent (that is, voice pause), and each voice source alternates between the two states. The voice stream generated by each voice source in the active period enters the data buffer at a constant rate. We assume that the capacity, which is denoted by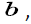 of the buffer in the system is finite. When the voice stream in the buffer reaches the upper bound
of the buffer in the system is finite. When the voice stream in the buffer reaches the upper bound  the newly entered voice stream will overflow and lead to the loss of voice information; when the buffer is empty and no new voice stream enters, then the system is idle.
the newly entered voice stream will overflow and lead to the loss of voice information; when the buffer is empty and no new voice stream enters, then the system is idle.
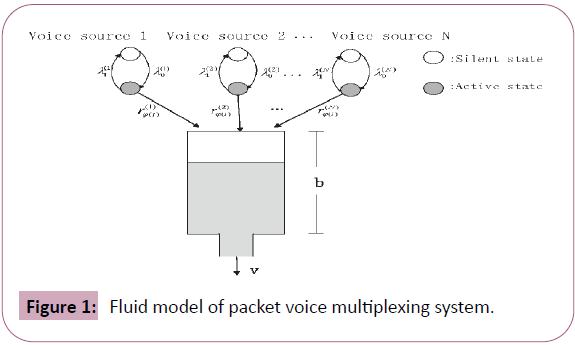
Figure 1: Fluid model of packet voice multiplexing system.
Consider the voice source 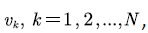 denote its state space by
denote its state space by  where
where  represents the silent state and
represents the silent state and 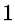 represents the active state. Suppose that the sojourn time of voice source
represents the active state. Suppose that the sojourn time of voice source 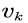 in state
in state 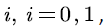 is the exponential distributed with mean
is the exponential distributed with mean 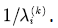 Thus, the evolution process of the voice source
Thus, the evolution process of the voice source 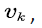 which is denoted by
which is denoted by 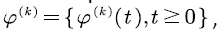 becomes a continuous time Markov chain (CTMC) on state space
becomes a continuous time Markov chain (CTMC) on state space 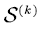 with transition rate matrix:
with transition rate matrix:
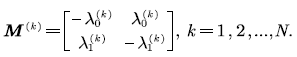
The voice stream generated by 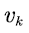 is injected into the buffer with time varying input rate. Specifically, at time t , the voice stream input rate is denoted by
is injected into the buffer with time varying input rate. Specifically, at time t , the voice stream input rate is denoted by 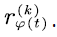 When the state of the voice source
When the state of the voice source 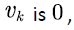 there is no voice stream enters multiplexing buffer, and the input rate is
there is no voice stream enters multiplexing buffer, and the input rate is 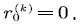 When the state of
When the state of 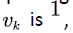 then
then 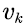 input the voice stream into the buffer at rate
input the voice stream into the buffer at rate 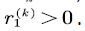 We denote
We denote 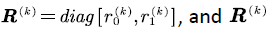 is referred to as input rate matrix of
is referred to as input rate matrix of 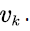
The voice stream in the multiplexing buffer is transmitted to the network system at a constant rate, which is denoted by 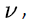 then the net input rate of
then the net input rate of 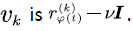 We let
We let 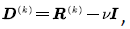 and we call
and we call 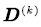 the net input matrix of
the net input matrix of 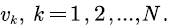
Now, define superposition process:
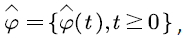
Where 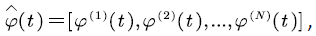 and refer to
and refer to 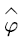 as the background process. In the packet voice multiplexing system, since N voice sources are independent of each other, then
as the background process. In the packet voice multiplexing system, since N voice sources are independent of each other, then 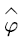 is CTMC on state space:
is CTMC on state space:
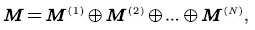
With the transition rate matrix:
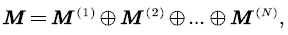
where  is Kronecker sum [11].
is Kronecker sum [11].
For the convenience of presentation, the states in S are numbered in sequence, and the state space is rewritten as 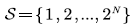 . Obviously,
. Obviously, 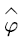 characterizes the evolution process of all voice sources in the system. Similarly, at time t , the input rate and the net input rate of
characterizes the evolution process of all voice sources in the system. Similarly, at time t , the input rate and the net input rate of 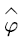 are denoted by
are denoted by 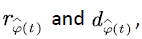 respectively. Then
respectively. Then 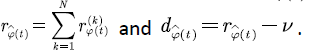 Thus, we can write the input rate and the net input rate matrices of
Thus, we can write the input rate and the net input rate matrices of 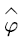 is:
is:
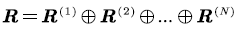
net input rate matrix is:
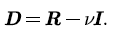
Let 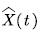 represent the amount (level) of voice stream in the multiplexing buffer at time t, we denote
represent the amount (level) of voice stream in the multiplexing buffer at time t, we denote 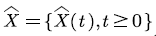 by the evolution process of the voice stream in the buffer, then
by the evolution process of the voice stream in the buffer, then 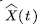 satisfies:
satisfies:
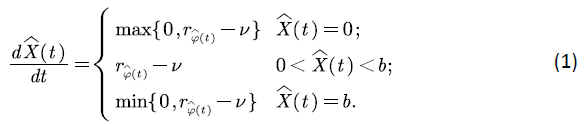
It can be seen from (1) that when 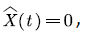 and the rate
and the rate 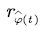 is less than
is less than 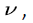 the buffer continues to be empty; when
the buffer continues to be empty; when 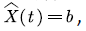 and the rate
and the rate 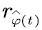 is greater than
is greater than 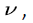 the voice stream in the buffer will remain; when
the voice stream in the buffer will remain; when 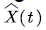 is between [0, b], the voice stream in the buffer changes at rate
is between [0, b], the voice stream in the buffer changes at rate 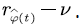 Without loss of generality, for any state
Without loss of generality, for any state 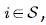 we assume
we assume 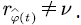
Let
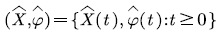
and it is easy to see that 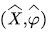
is a SFM model and it is describe the packet voice multiplexing system model under consideration in this paper. In SFM 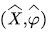 , the level process
, the level process 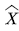 describes the change process of the voice stream level in the multiplexing buffer. Because the multiplexing buffer is finite, when the voice stream reaches the level b, overflow will occur; when the voice stream level is reduced to 0, the multiplexing buffer is empty. The background process
describes the change process of the voice stream level in the multiplexing buffer. Because the multiplexing buffer is finite, when the voice stream reaches the level b, overflow will occur; when the voice stream level is reduced to 0, the multiplexing buffer is empty. The background process 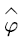 describes the change of the voice source state, which affects the input rate of the voice multiplexing system, and controls the change of the voice stream level
describes the change of the voice source state, which affects the input rate of the voice multiplexing system, and controls the change of the voice stream level 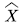 in the multiplexing buffer.
in the multiplexing buffer.
In the packet voice multiplexing system, the multiplexing buffer size and the number of voice sources make an important impact on the performance metrics of the system. The main goal of this paper is to derive the exact expressions of overflow probability and idle probability of the packet voice multiplexing system 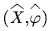 , and investigate numerically the setting of the optimal buffer size and the optimal number of users that can be accommodated given the maximum tolerable overflow probability.
, and investigate numerically the setting of the optimal buffer size and the optimal number of users that can be accommodated given the maximum tolerable overflow probability.
Results and Discussion
Model analysis
Before our analysis, we first give the following definitions.
In SFM 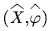 we define the stationary probability density and boundary probability
we define the stationary probability density and boundary probability
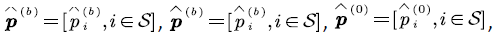
where:
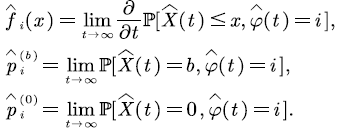
According to the backward equation, the stationary probability (density) of SFM 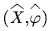 satisfies:
satisfies:

where 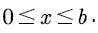 Let
Let
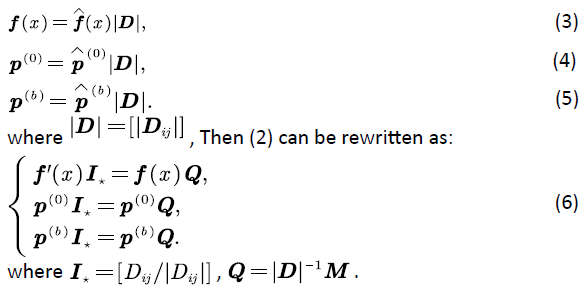
It can be seen from (6) that the SFM 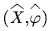 is transformed into a new SFM with net input rate matrix
is transformed into a new SFM with net input rate matrix 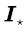 (that is, the net input rate is ±1), and the transition rate matrix Q . We denote this new SFM by
(that is, the net input rate is ±1), and the transition rate matrix Q . We denote this new SFM by 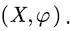 Now, we mainly study SFM
Now, we mainly study SFM 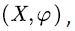 and the performance metrics of the original SFM
and the performance metrics of the original SFM 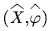 can be obtained based on (3-5).
can be obtained based on (3-5).
According to the sign of the net input rate, the state space S is divided into two disjoint subsets: 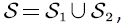 where:
where:
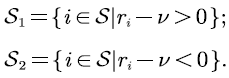
Based on the division of the state, the matrices  can be written in the following block form accordingly:
can be written in the following block form accordingly:
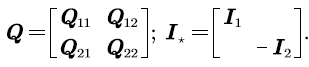
Similarly,  can be written in block form:
can be written in block form:
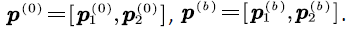
When the voice stream in the buffer reaches the upper bound b , and the net input rate is negative at this time, the voice stream in the buffer cannot be maintained at the upper bound, therefore, 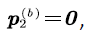 and we call
and we call 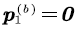 the overflow probability; Similarly, when the multiplexing buffer is empty and the net input rate is positive, the voice stream in the buffer cannot be empty, therefore,
the overflow probability; Similarly, when the multiplexing buffer is empty and the net input rate is positive, the voice stream in the buffer cannot be empty, therefore, 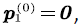 and we call
and we call 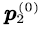 the idle probability.
the idle probability.
To analyze the overflow probability and idle probability of the voice multiplexing system model, we define First Passage Time (FPT) as follows.
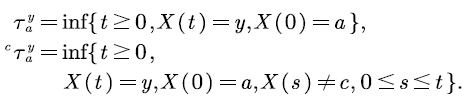
We are interested in the two first passage times 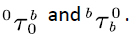 That is,
That is, 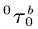 is the first time epoch that the level process reaches the buffer upper bound b with initial level 0 before the buffer is empty; and
is the first time epoch that the level process reaches the buffer upper bound b with initial level 0 before the buffer is empty; and 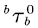 is the first time epoch that the level process starts from the buffer upper bound level 0, and first reaches the level 0 without returning level b.
is the first time epoch that the level process starts from the buffer upper bound level 0, and first reaches the level 0 without returning level b.
We define the following probability matrix of FPT as 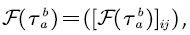 and denote its
and denote its 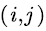 -th elements by:
-th elements by:
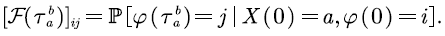
Obviously, 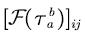 represents the probability that the SFM
represents the probability that the SFM 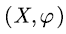 starts from state
starts from state 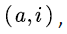 and arrives at
and arrives at 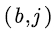 for the first time.
for the first time.
Similarly, we define matrix 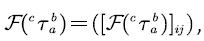 and denote its ( i,j ) -th elements by:
and denote its ( i,j ) -th elements by:
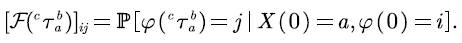
In order to simplify the calculation, the level-reverse process is denoted by:
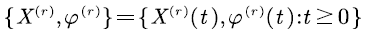
which is considered by [12,13]. The level-reverse SFM 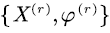 has the same transition rate matrix of the SFM
has the same transition rate matrix of the SFM 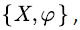 but the net input rate of the state is exactly the opposite. That is, in
but the net input rate of the state is exactly the opposite. That is, in  let the net input rate be
let the net input rate be 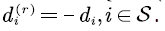
For the convenience of description, a quantum 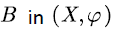 is correspondingly denoted by
is correspondingly denoted by 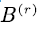 in the level-reverse process
in the level-reverse process 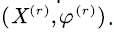
According to the division of state, 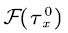 has the following matrix block form:
has the following matrix block form:
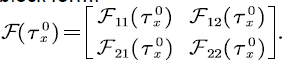
Because the level process X can only reach the level 0 for the first time in the state set  therefore:
therefore:
The following lemma gives the expressions of  and
and 
Lemma 1 [14] For the SFM  and
and 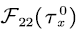 have the following expressions:
have the following expressions:

Matrix Φ satisfies the following Riccati equation [12].
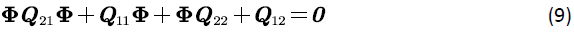
The literature [15-17] gives an effective algorithm for solving Φ in the (9). It can be seen from the above expression that after Φ and 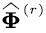 are given, all the quantities are available.
are given, all the quantities are available.
Similarly, we have the following conclusions for the block matrices 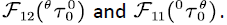
Lemma 2 [14] For the SFM 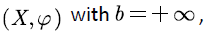 the following equation holds:
the following equation holds:
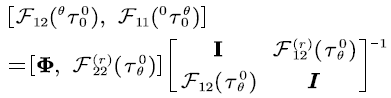
Based on the above two lemmas, we begin to derive the stationary boundary probability of the SFM 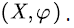
As shown in Figure 2, we truncate 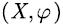 and only remain the path sample of the system on the boundary level 0 and the boundary level b. The state space of the truncated process can be written as
and only remain the path sample of the system on the boundary level 0 and the boundary level b. The state space of the truncated process can be written as
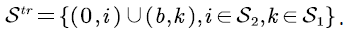
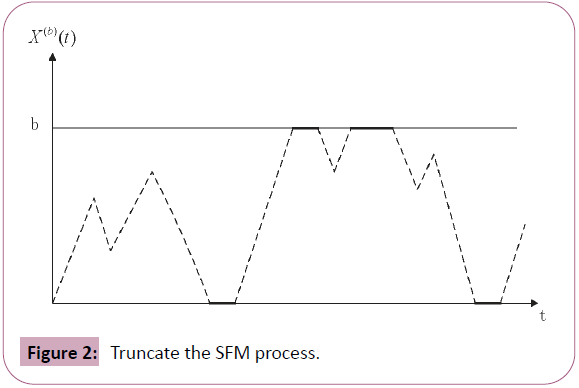
Figure 2: Truncate the SFM process.
We consider the transition rate of the truncated process in the interval 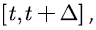 let Δ be small enough. Let
let Δ be small enough. Let 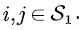 At the time t, we assume the state of the truncated process is ( b,i ), then two cases will be occurred when the truncation process transits to state ( b,j ) from state ( b,i ) :
At the time t, we assume the state of the truncated process is ( b,i ), then two cases will be occurred when the truncation process transits to state ( b,j ) from state ( b,i ) :
The truncated process transits directly from state ( b,i ) to state ( b,j ) with probability 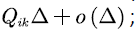
The truncation process transits from state ( b,i ) to state ( b,k ), where 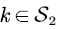 with probability
with probability 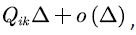 and then the process starts from state ( b,k ) to state ( b,j ), while during the transition, the sample path cannot hits the level . From lemma 2, the probability of this event is
and then the process starts from state ( b,k ) to state ( b,j ), while during the transition, the sample path cannot hits the level . From lemma 2, the probability of this event is 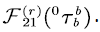
Thus, the transition rate matrix from 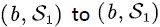 has the following form:
has the following form: 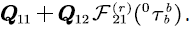
Similarly, we can construct the transition rate of truncation process in the following block form:
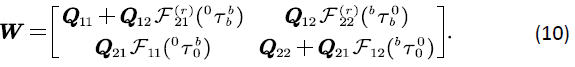
At the same time, we notice that when the fluid queue is at the middle level, the time for upward transition is equal to the time for downward transition [10]. Therefore:
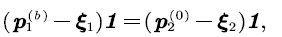
where 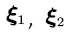 are the stationary distributions of background processes, that is, we have
are the stationary distributions of background processes, that is, we have 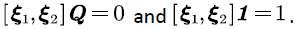
Now we can solve the following equation to obtain the stationary boundary probability 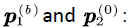
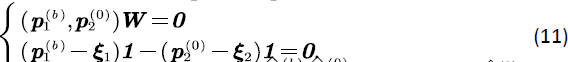
It can be seen from (2)-(5) that 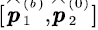 and
and 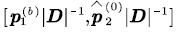 are proportional to each other, then we have:
are proportional to each other, then we have:
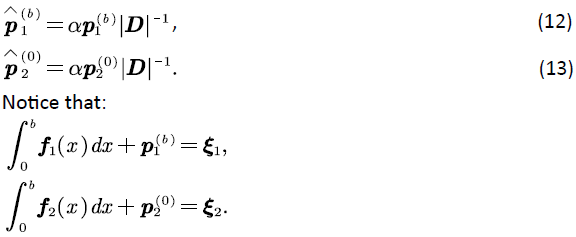
Thus, α can be determined by the following equation:
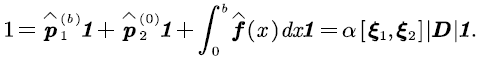
From the above formula, we have:

Now, we obtain the overflow and idle probabilities of the buffer in the packet voice multiplexing system 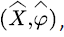 we summary the corresponding algorithms in Algorithm 1 (Table 1).
we summary the corresponding algorithms in Algorithm 1 (Table 1).
| S. No |
Algorithm 1 Overflow and idle probabilities algorithm of the packet voice multiplexing system |
| 1 |
Step 1. Divide 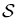 into into 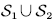 , construct block matrix Q . , construct block matrix Q . |
| 2 |
Step 2. Use (9) to obtain Φ. |
| 3 |
Step 3. Use lemma 1 to obtain 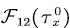 and and 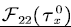 . . |
| 4 |
Step 4. Use lemma 2 to obtain 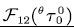 and and 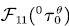 . . |
| 5 |
Step 5. Construct transition rate matrix W base on step 3 and step 4. |
| 6 |
Step 6. Obtain 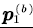 and and 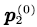 base on (11). base on (11). |
| 7 |
Step 7. Obtain α base on (14). |
| 8 |
Step 8. Finally, obtain 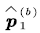 and and 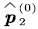 base on (4)-(5). base on (4)-(5). |
Table 1: Overflow and idle probability algorithm of buffer in packet voice multiplexing system.
Numerical example
In this section, we will give numerical examples to illustrate our analytical conclusions.
Numerical setting: Consider a small experimental scenario of multi-user voice stream transmission. We assume N identical and independent users 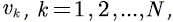 in the scenario. The voice signal is transmitted to the channel at rate
in the scenario. The voice signal is transmitted to the channel at rate 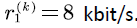 Since the voice multiplexing system adopts the principle of frequency division multiplexing, the frequency range of the voice signal is 300-400 Hz, and the signal-noise ratio of the general link is 30 dB [18]. So by Shannon formula, the transmission rate of the voice signal to the network system is about v = 31 kbit/s. Suppose that the average sojourn time of the voice in state ``active" is 3 min, and the average time in state ``silent" is 2 min. Then the transition rate matrix is :
Since the voice multiplexing system adopts the principle of frequency division multiplexing, the frequency range of the voice signal is 300-400 Hz, and the signal-noise ratio of the general link is 30 dB [18]. So by Shannon formula, the transmission rate of the voice signal to the network system is about v = 31 kbit/s. Suppose that the average sojourn time of the voice in state ``active" is 3 min, and the average time in state ``silent" is 2 min. Then the transition rate matrix is :
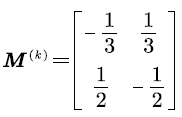
the input rate matrix is 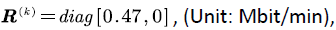 for k = 1, 2, ..., N . According to the theoretical findings developed in this paper, we obtain and describe the corresponding numerical results in the following figure.
for k = 1, 2, ..., N . According to the theoretical findings developed in this paper, we obtain and describe the corresponding numerical results in the following figure.
Numerical analysis
Figure 3 shows the relationship between the overflow probability and the buffer size under different number of users. The abscissa represents the size of the buffer, and the ordinate represents the overflow probability of the packet voice multiplexing system. As can be seen from Figure 3, given the same buffer size, the overflow probability increases with the increasing the number of users. It can also be noticed that given the number of uses, the overflow probability decreases when the buffer capacity increases. However, as the buffer size becomes larger and larger, the impact becomes smaller and smaller. This observation suggests that simply increasing buffer size is not a suitable way to decrease the overflow probability, and the number of users need to be under consideration.
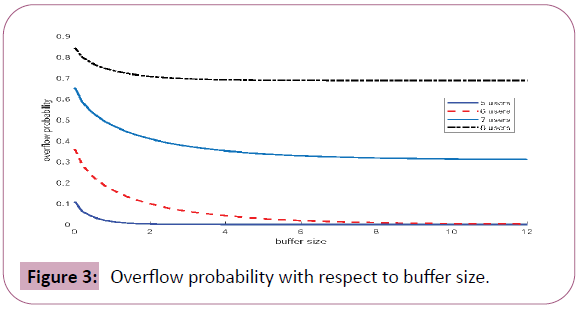
Figure 3: Overflow probability with respect to buffer size.
In Figure 4 we can see that given the number of users, when the buffer size increases, as expected, the idle probability of the system decreases. This observation can be explained by the fact that as the buffer size increases, the overflow probability becomes smaller, and then the more voice information of the system has to process, so the idle probability decreases with the increasing of the buffer size. When given the buffer size, we can see that the idle probability decreases with the increasing of the number of users. This because as the number of users increases, the more voice stream in the buffer, and then the more voice information of the system has to process, so the idle probability decreases with the increasing of the number of users.
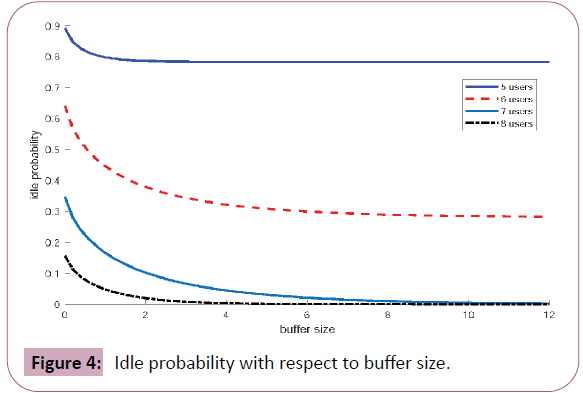
Figure 4: Idle probability with respect to buffer size.
System parameter setting
Based on the above scenario settings, as an application, in the following we illustrate, given the maximum tolerable overflow probability, how to design the two important parameters of the packet voice multiplexing system, i.e., the buffer size and the maximum number of users that system can accommodate (Figure 5). We should first determine the maximum number of users the system can accommodate, this because the overflow probability has not been significantly impacted by the changes of the buffer size (Figure 3).
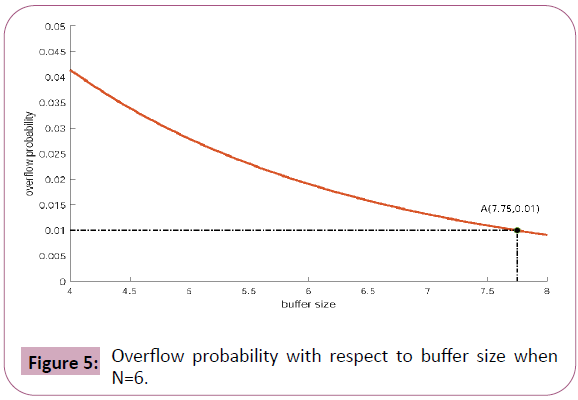
Figure 5: Overflow probability with respect to buffer size when N=6.
Conclusion
This paper investigates the overflow and idle probabilities of the packet voice multiplexing system based on the framework of SFM. We truncate the system sample path, and derive the overflow and the idle probabilities by the matrix-analytic methodology. Numerical investigation of the theoretical results is performed, as an application, the optimal buffer size and the maximum number of users is investigated with the maximum tolerable overflow probability constraint. The theoretical findings in this paper are of important guiding significance for the design and management of the packet voice multiplexing systems. In future work, we can extend the system model proposed in this paper, and analyze the important performance metrics of the packet voice multiplexing system with priority.
Acknowledgements
The paper is supported by National Natural Science Foundation of China under Grant No. 61761008, No. 2018GXNSFAA281238, and the project of Guangxi Colleges and Universities Key Laboratory of Mathematical and Statistical Model under Grant No. 2017GXKLM002.
References
- Kulik I, Trinh TA (2013) Evaluation of the quality of experience for 3D future internet multimedia. Acta Polytechnica Hungarica 10: 25-42.
- Pitts JM, Schormans JA (2001) Introduction to IP and ATM design and performance. John Wiley Sons Limited, 2001.
- Anick D, Mitra D, Sondhi MM (1982) Stochastic theory of a data?handling system with multiple sources. Bell Syst Tech J 61: 1871-94.
- Estepa A, Estepa R (2008) Accurate resource estimation for homogeneous VoIP aggregated traffic. Comput Netw 52: 2505-17.
- Arunachalam V, Gupta V, Dharmaraja S (2010) A fluid queue modulated by two independent birth-death processes. Comput Math Appl 60: 2433-44.
- Xu X, Zhao Y, Geng J, Jin S (2013) Analysis of the fluid model driven by an M/PH/1 queue. J Inf Comput Sci 10: 3489-96.
- Trenkic B, Mitic D, Lebl A, Markov Z (2015) Fluid flow approximation of the mean buffer occupancy in a packet-speech multiplexer. J Internet Technol 16: 1211-7.
- Trenkic B, Stefanovic M (2011) One approach in evaluating the overflow probability using the infinite fluid-flow queue. FU Elec Energ 24: 1-8.
- Kulkarni VG (1997) Fluid models for single buffer systems. Frontiers in queueing: Models and applications in science and engineering: 321:338.
- Da Silva Soares A (2005) Fluid queues: Building upon the analogy with QBD processes. Di-Fusion 1: 174.
- Bean NG, O’Reilly MM, Taylor PG (2008) Algorithms for the Laplace-Stieltjes transforms of first return times for stochastic fluid flows. Methodol Comput Appl Probab 10: 381-408.
- Ahn S, Badescu AL, Ramaswami V (2007) Time dependent analysis of finite buffer fluid flows and risk models with a dividend barrier. Queueing Syst 55: 207-22.
- Ramaswami V (2006) Passage times in fluid models with application to risk processes. Methodol Comput Appl Probab 8: 497-515.
- Bean NG, O’Reilly MM (2008) Performance measures of a multi-layer Markovian fluid model. Ann Oper Res 160: 99-120.
- Ramaswami V (1999) Matrix analytic methods for stochastic fluid flows. Teletraffic Sci Eng 2: 1019-30.
- Da Silva Soares A, Latouche G (2002) Further results on the similarity between fluid queues and QBDs. Matrix Anal Methods: 89-106.
- Stern TE, Elwalid AI (1991) Analysis of separable Markov-modulated rate models for information-handling systems. Adv Appl Probab:105-39.
- Hofner TC (2000) Defining and testing dynamic ADC parameters. Microwaves RF 162: 75-84.

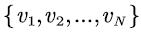 . Each voice source has two states: active (that is, voice call phase) and silent (that is, voice pause), and each voice source alternates between the two states. The voice stream generated by each voice source in the active period enters the data buffer at a constant rate. We assume that the capacity, which is denoted by
. Each voice source has two states: active (that is, voice call phase) and silent (that is, voice pause), and each voice source alternates between the two states. The voice stream generated by each voice source in the active period enters the data buffer at a constant rate. We assume that the capacity, which is denoted by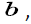 of the buffer in the system is finite. When the voice stream in the buffer reaches the upper bound
of the buffer in the system is finite. When the voice stream in the buffer reaches the upper bound 
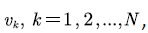 denote its state space by
denote its state space by 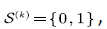 where
where 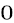 represents the silent state and
represents the silent state and 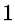 represents the active state. Suppose that the sojourn time of voice source
represents the active state. Suppose that the sojourn time of voice source 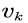 in state
in state 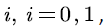 is the exponential distributed with mean
is the exponential distributed with mean 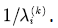 Thus, the evolution process of the voice source
Thus, the evolution process of the voice source 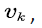 which is denoted by
which is denoted by 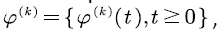 becomes a continuous time Markov chain (CTMC) on state space
becomes a continuous time Markov chain (CTMC) on state space 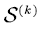 with transition rate matrix:
with transition rate matrix: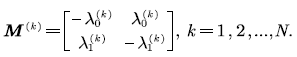
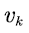 is injected into the buffer with time varying input rate. Specifically, at time t , the voice stream input rate is denoted by
is injected into the buffer with time varying input rate. Specifically, at time t , the voice stream input rate is denoted by 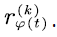 When the state of the voice source
When the state of the voice source 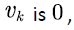 there is no voice stream enters multiplexing buffer, and the input rate is
there is no voice stream enters multiplexing buffer, and the input rate is 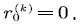 When the state of
When the state of 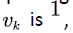 then
then 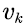 input the voice stream into the buffer at rate
input the voice stream into the buffer at rate 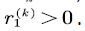 We denote
We denote 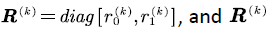 is referred to as input rate matrix of
is referred to as input rate matrix of 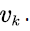
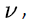 then the net input rate of
then the net input rate of 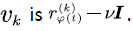 We let
We let 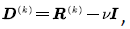 and we call
and we call 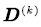 the net input matrix of
the net input matrix of 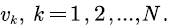
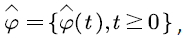
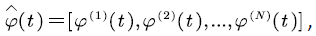 and refer to
and refer to 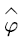 as the background process. In the packet voice multiplexing system, since N voice sources are independent of each other, then
as the background process. In the packet voice multiplexing system, since N voice sources are independent of each other, then 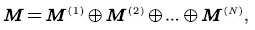
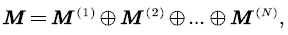
 is Kronecker sum [
is Kronecker sum [ . Obviously,
. Obviously, 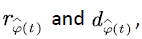 respectively. Then
respectively. Then 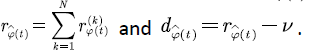 Thus, we can write the input rate and the net input rate matrices of
Thus, we can write the input rate and the net input rate matrices of 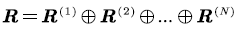
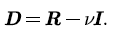
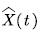 represent the amount (level) of voice stream in the multiplexing buffer at time t, we denote
represent the amount (level) of voice stream in the multiplexing buffer at time t, we denote 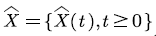 by the evolution process of the voice stream in the buffer, then
by the evolution process of the voice stream in the buffer, then 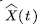 satisfies:
satisfies: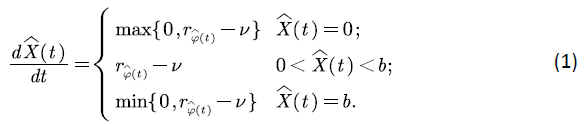
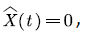 and the rate
and the rate 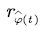 is less than
is less than 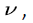 the buffer continues to be empty; when
the buffer continues to be empty; when 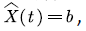 and the rate
and the rate 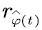 is greater than
is greater than 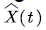 is between [0, b], the voice stream in the buffer changes at rate
is between [0, b], the voice stream in the buffer changes at rate 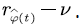 Without loss of generality, for any state
Without loss of generality, for any state 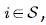 we assume
we assume 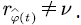
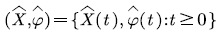
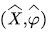
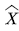 describes the change process of the voice stream level in the multiplexing buffer. Because the multiplexing buffer is finite, when the voice stream reaches the level b, overflow will occur; when the voice stream level is reduced to 0, the multiplexing buffer is empty. The background process
describes the change process of the voice stream level in the multiplexing buffer. Because the multiplexing buffer is finite, when the voice stream reaches the level b, overflow will occur; when the voice stream level is reduced to 0, the multiplexing buffer is empty. The background process 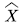 in the multiplexing buffer.
in the multiplexing buffer.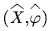 , and investigate numerically the setting of the optimal buffer size and the optimal number of users that can be accommodated given the maximum tolerable overflow probability.
, and investigate numerically the setting of the optimal buffer size and the optimal number of users that can be accommodated given the maximum tolerable overflow probability.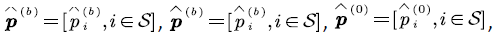
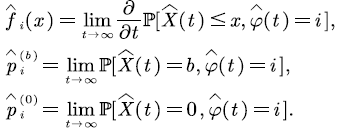

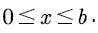 Let
Let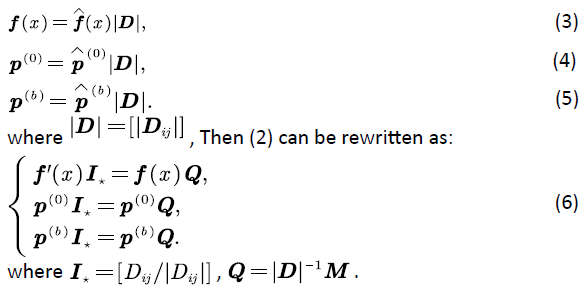
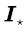 (that is, the net input rate is ±1), and the transition rate matrix Q . We denote this new SFM by
(that is, the net input rate is ±1), and the transition rate matrix Q . We denote this new SFM by 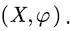 Now, we mainly study SFM
Now, we mainly study SFM 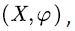 and the performance metrics of the original SFM
and the performance metrics of the original SFM 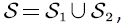 where:
where: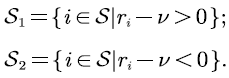
 can be written in the following block form accordingly:
can be written in the following block form accordingly: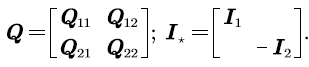
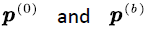 can be written in block form:
can be written in block form: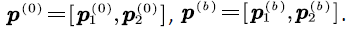
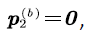 and we call
and we call 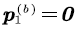 the overflow probability; Similarly, when the multiplexing buffer is empty and the net input rate is positive, the voice stream in the buffer cannot be empty, therefore,
the overflow probability; Similarly, when the multiplexing buffer is empty and the net input rate is positive, the voice stream in the buffer cannot be empty, therefore, 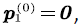 and we call
and we call 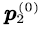 the idle probability.
the idle probability.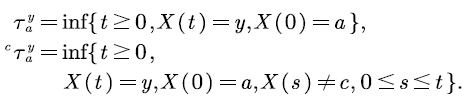
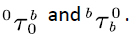 That is,
That is, 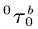 is the first time epoch that the level process reaches the buffer upper bound b with initial level 0 before the buffer is empty; and
is the first time epoch that the level process reaches the buffer upper bound b with initial level 0 before the buffer is empty; and 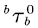 is the first time epoch that the level process starts from the buffer upper bound level 0, and first reaches the level 0 without returning level b.
is the first time epoch that the level process starts from the buffer upper bound level 0, and first reaches the level 0 without returning level b.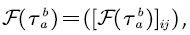 and denote its
and denote its 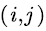 -th elements by:
-th elements by: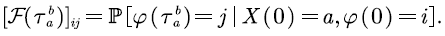
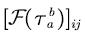 represents the probability that the SFM
represents the probability that the SFM 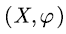 starts from state
starts from state 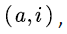 and arrives at
and arrives at 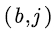 for the first time.
for the first time.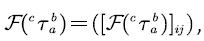 and denote its ( i,j ) -th elements by:
and denote its ( i,j ) -th elements by: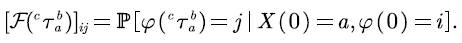
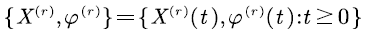
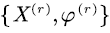 has the same transition rate matrix of the SFM
has the same transition rate matrix of the SFM 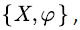 but the net input rate of the state is exactly the opposite. That is, in
but the net input rate of the state is exactly the opposite. That is, in 
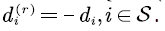
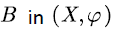 is correspondingly denoted by
is correspondingly denoted by 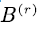 in the level-reverse process
in the level-reverse process 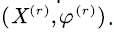
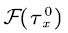 has the following matrix block form:
has the following matrix block form: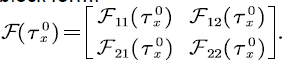
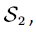 therefore:
therefore: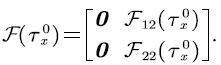
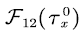 and
and 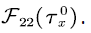
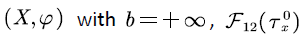 and
and 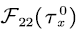 have the following expressions:
have the following expressions:
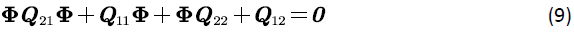
 are given, all the quantities are available.
are given, all the quantities are available.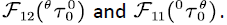
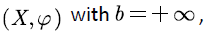 the following equation holds:
the following equation holds: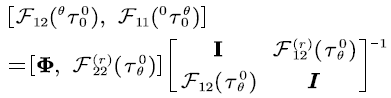
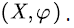
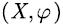 and only remain the path sample of the system on the boundary level 0 and the boundary level b. The state space of the truncated process can be written as
and only remain the path sample of the system on the boundary level 0 and the boundary level b. The state space of the truncated process can be written as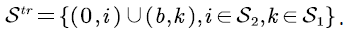

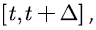 let Δ be small enough. Let
let Δ be small enough. Let 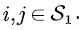 At the time t, we assume the state of the truncated process is ( b,i ), then two cases will be occurred when the truncation process transits to state ( b,j ) from state ( b,i ) :
At the time t, we assume the state of the truncated process is ( b,i ), then two cases will be occurred when the truncation process transits to state ( b,j ) from state ( b,i ) :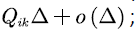
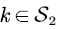 with probability
with probability 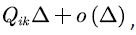 and then the process starts from state ( b,k ) to state ( b,j ), while during the transition, the sample path cannot hits the level . From lemma 2, the probability of this event is
and then the process starts from state ( b,k ) to state ( b,j ), while during the transition, the sample path cannot hits the level . From lemma 2, the probability of this event is 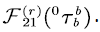
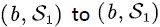 has the following form:
has the following form: 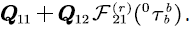
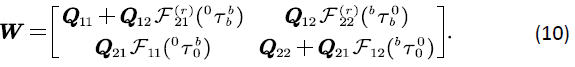
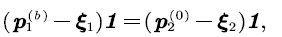
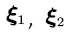 are the stationary distributions of background processes, that is, we have
are the stationary distributions of background processes, that is, we have 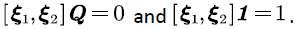
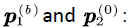
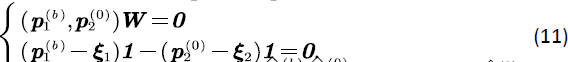
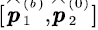 and
and 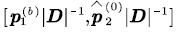 are proportional to each other, then we have:
are proportional to each other, then we have: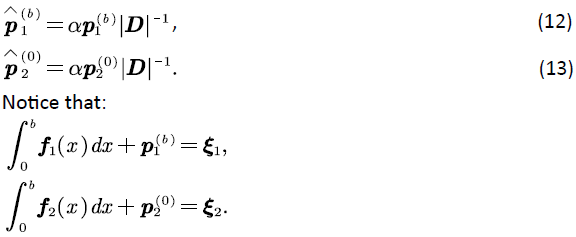
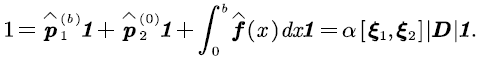

 we summary the corresponding algorithms in Algorithm 1 (Table 1).
we summary the corresponding algorithms in Algorithm 1 (Table 1).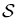 into
into 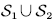 , construct block matrix Q .
, construct block matrix Q .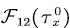 and
and 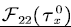 .
.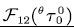 and
and 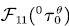 .
.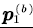 and
and 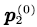 base on (11).
base on (11).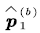 and
and 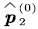 base on (4)-(5).
base on (4)-(5).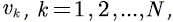 in the scenario. The voice signal is transmitted to the channel at rate
in the scenario. The voice signal is transmitted to the channel at rate 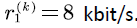 Since the voice multiplexing system adopts the principle of frequency division multiplexing, the frequency range of the voice signal is 300-400 Hz, and the signal-noise ratio of the general link is 30 dB [
Since the voice multiplexing system adopts the principle of frequency division multiplexing, the frequency range of the voice signal is 300-400 Hz, and the signal-noise ratio of the general link is 30 dB [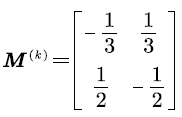
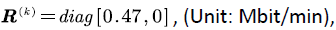 for k = 1, 2, ..., N . According to the theoretical findings developed in this paper, we obtain and describe the corresponding numerical results in the following figure.
for k = 1, 2, ..., N . According to the theoretical findings developed in this paper, we obtain and describe the corresponding numerical results in the following figure.