Keywords
Sextic equation; Polynomials; Factorized
Introduction
The work of Abel (1826) and Galois (1832) have shown that general polynomials of degree five and greater cannot be solved in radicals. Galois gave a more rigorous proof of the impossibility of solving these higher degree equations using group theory. After the work of these two researchers, there have been attempts to obtain algebraic solution using symbolic coefficients. In modern algebra, for example, the general quintic equation has been solved using the Bring Radicals, while the general sextic equation has been solved in terms of Kampe de Feriet Functions.
The genesis to the modern approach to solving algebraic equations can be traced back to work of Francois Viète, a French mathematician. It was Francois Viète who set into course the path of solving higher degree polynomial equations by relating its coefficients to the roots via elementary symmetric equations. Louis Lagrange introduced Resolvents and they were systematically used by Galois as a tool for seeking specific solution of higher degree polynomials. The Lagrange and Galois resolvents were successful in establishing a unified approach to solving quadratic, cubic, and quartic equations, but failed to achieve formulae for general algebraic equations greater than four.
Either the approach employed by Galois and the forerunners of the theory was inappropriate in achieving a general radical solution of higher degree polynomials or such a solution is impossible. Other possible approaches for obtaining radical solution need to be fully explored before coming to conclusions of impossibility. Impossibility theorems can be arrived at using dead end approaches to solutions.
In an attempt to solve the general quartic equation, Lodvico Ferrari factorized the quartic equation to two quadratic factors. He then got a way to correlate the unknown coefficients of the quadratic factors to the known coefficients of the general quartic equation. Higher degree polynomial should be reducible if a rational or radical formulae can be established connecting the unknown to known parameters. Galois Theory failed to explore connections that may exist between known and unknown parameters in possible solvable factorized forms that may exist in higher degree general polynomial equations. Galois Theory instead looks into solvable connections between the roots and coefficients and attempts to solve the fundamental symmetric equations. The Galois resolvent magnifies the problem of achieving radical solutions general algebraic equations of degree five and above to levels of impossibility.
The problem of obtaining radical solution of higher degree polynomial equations needs to be to be lessened through some intermediate connections that will generate lower degree auxiliary solvable factors. This calls for some forms of solvable decomposition of higher degree polynomial equations.
In 2011, Edward Thabo Motlotle achieved a radical solution of the Bring-Jerrard quintic equation with the aid of Newton’s sum formula. The problem with the method employed by him is that it is very involving and dampens any hope of achieving radical solution of higher degree polynomial equations. Between 2013 and 2017, Buya SB made attempts to contribute further to these solutions. In his yet to be published work, Buya SB further showed that radical solution of the general quintic equation is possible without a Tschirnhausen. These results contradict Abel’s impossibility theorem and Galois Theory.
In this research a contribution will be made in deriving radical solution of the general sextic equation. Many have attempted to obtain algebraic solution of sextic equations. One noteworthy work was done by Raghavendra G. Kulkarni, in which he attempted the solution of the general sextic equation by method of decomposition. However, he failed to correlate all the unknown coefficients, he introduced to the real coefficients of the general sextic equation. He attributed the inability to correlate the coefficients to Abel’s impossibility theorem. He then introduced supplementary coefficients that resulted in some original coefficients losing their independence. Thus, he failed to achieve a general solution of the general sextic equation.
In paper entitled “Trinomial sextic equation, its algebraic solution to solvable factorized form,” Buya SB showed that the factorization method is a most appropriate method for solving higher degree algebraic equations, provided the appropriate factorized form is selected.
In this paper, we show a possible factorized form that can be used to obtain a general radical solution of the general sextic equation. The auxiliary factors derived are quadratic and quartic. The unknown coefficients introduced in these factors are correlated to the original parameters before obtaining the solution of auxiliary equations. This means a radical solution of the unknown coefficients has first to be to be sought for in terms of finite addition, subtraction, multiplication, and division of the known coefficients of the original equation [1-6]. The radical solution of the general sextic equation then follows.
Methodology
Factorized form one
The general sextic equation takes the form:
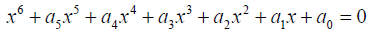 (1)
(1)
The factorization method is a good candidate method for solving the general sextic equation algebraically. The big task is to identify a solvable form of such an equation.
A solvable factorized form of the above equation can be given by:
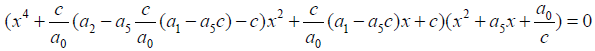 (2)
(2)
Expanding equation 2:
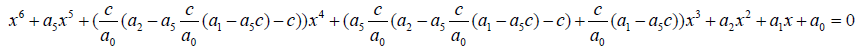 (3)
(3)
Equating x4 coefficients
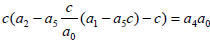 (4)
(4)
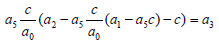 (5)
(5)
For a3 to be independent then:
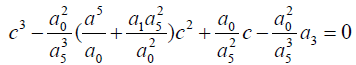 (6)
(6)
Obtain the Cardano solution of c.
To obtain the dependent value of 4 a then substitute the solution of 6 into 4
Take:
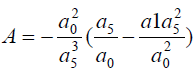 (7)
(7)
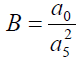 (8)
(8)
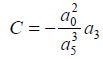 (9)
(9)
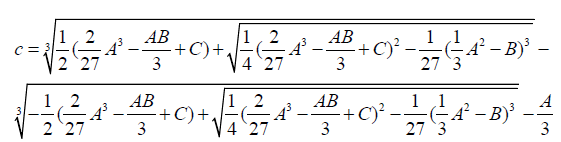 (10)
(10)
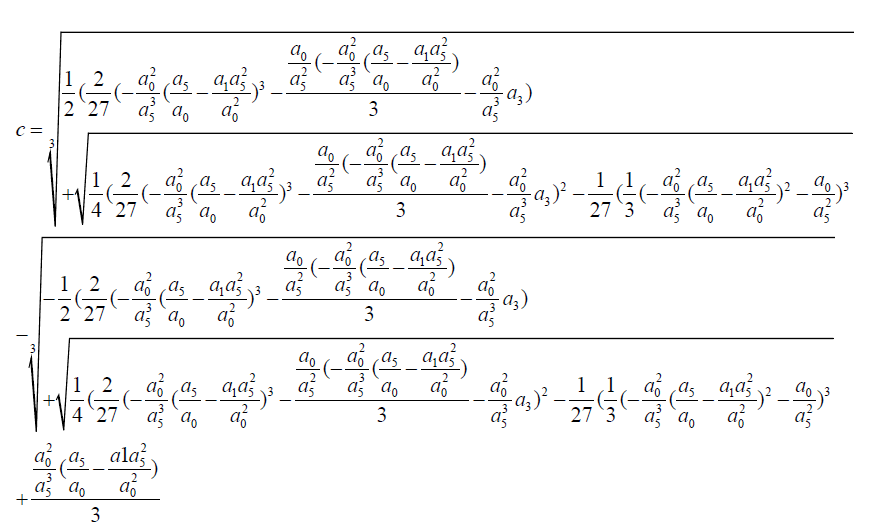 (11)
(11)
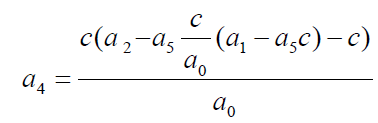 (12)
(12)
a4 is a dependent parameter
The auxiliary quadratic equation of the above sextic equation is given by:
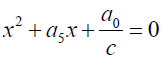
In this case two of the roots of the sextic equation are given by:
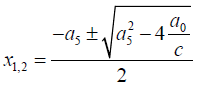
In this research, we are interested in obtaining a radical solution of the general sextic equation without a Tschirnhausen transformation. The a4 coefficient is not independent. Therefore, the above factorization falls short of this requirement.
Factorized form two
The general sextic equation takes the form:
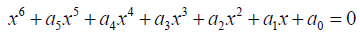 (1)
(1)
The factorization method is a good candidate method for solving the general sextic equation algebraically. The big task is to identify a solvable form of such an equation.
A solvable factorized form of the above equation can be given by:
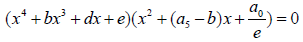 (2)
(2)
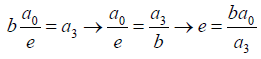 (3)
(3)
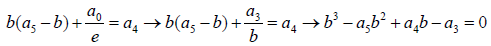 (4)
(4)
Obtain the Cardano solution of 4
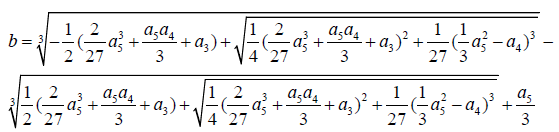 (4)
(4)
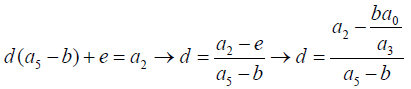 (5)
(5)
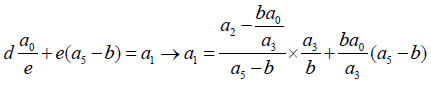 (6)
(6)
a1 is a dependent parameter. The formulae obtained as a result of the above factorization fall short of obtaining radical solution of the general sextic equation without a Tschirnhausen transformation.
Factorized form 3
The general sextic equation takes the form:
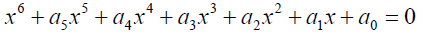 (1)
(1)
The factorization method is a good candidate method for solving the general sextic equation algebraically. The big task is to identify a solvable form of such an equation.
A solvable factorized form of the above equation can be given by:
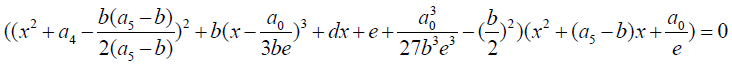 (2)
(2)
Equating coefficients:
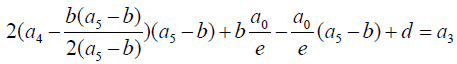 (3)
(3)
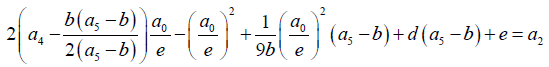 (4)
(4)
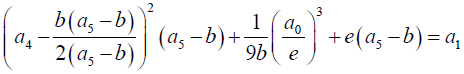 (5)
(5)
If in equation 3:
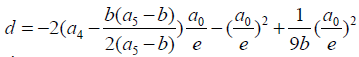 (6)
(6)
Then
e=a2 (7)
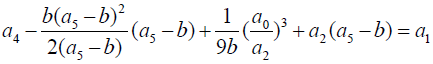
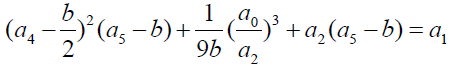 (8)
(8)
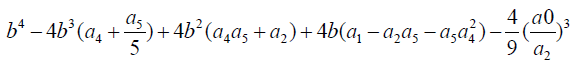 (9)
(9)
If we let we take:
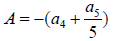 (10)
(10)
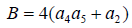 (11)
(11)
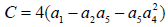 (12)
(12)
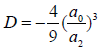 (13)
(13)
Then, the equation 9 takes the form:
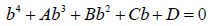 (14)
(14)
Take 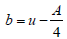 (15)
(15)
Then:
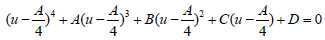 (16)
(16)
After regrouping the terms, the equation 16 takes the depressed quartic equation form:
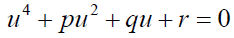 (17)
(17)
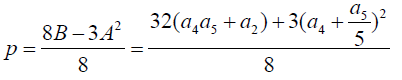 (18)
(18)
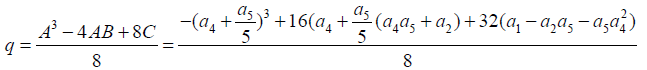 (19)
(19)
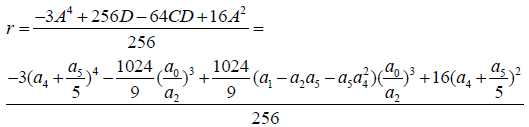 (20)
(20)
Equation 17 can be written in the form 21 below to enable determination of the roots of u.
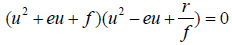 (21)
(21)
Where:
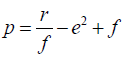 (22)
(22)
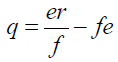 (23)
(23)
Multiplying 22 by e and rearranging: (24)
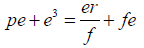 (25)
(25)
Adding 25 to 23:
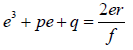 (26)
(26)
Subtracting 25 with 23:
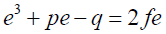 (27)
(27)
Multiplying together 27 and 28:
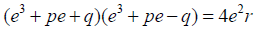 (28)
(28)
Equation 28 can be simplified to the solvable form:
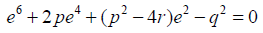 (29)
(29)
Take:
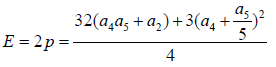 (30)
(30)
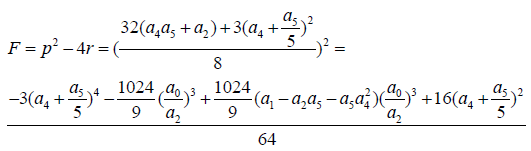 (31)
(31)
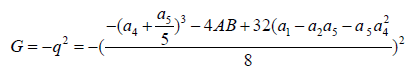 (32)
(32)
Then, the equation 29 takes the form:
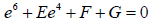 (33)
(33)
Take e2 = v (34)
Then the equation 34 takes the form:
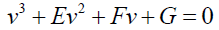 (35)
(35)
Take:
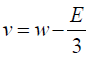 (36)
(36)
Then the equation 35 takes the form:
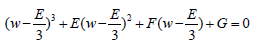 (37)
(37)
On expanding the equation 37:
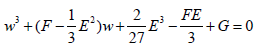 (38)
(38)
One of the roots of equation 36 is given by:
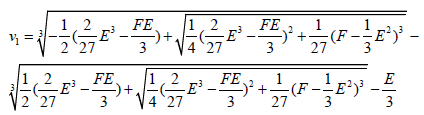 (39)
(39)
One of the roots of e in equation 34 is given by:
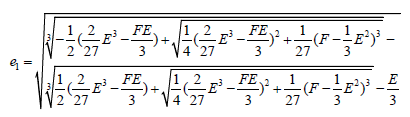 (40)
(40)
From equation 27:
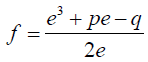 (41)
(41)
Equation 21 can be written in the form 42 below:
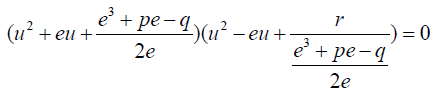 (42)
(42)
The roots of u are given by:
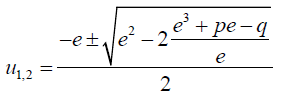 (43)
(43)
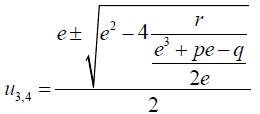 (44)
(44)
The roots of b in equation 9 are given by:
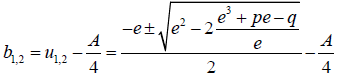 (45)
(45)
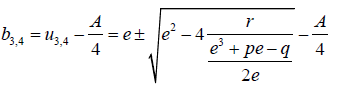 (46)
(46)
The radical solution of the quantity b enables determination of quantity d in equation 6.
The auxiliary quadratic equation of the factorized sextic equation is:
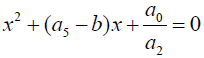 (47)
(47)
Two of the roots of the sextic equation are:
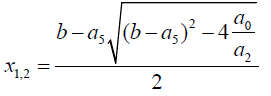 (48)
(48)
The other roots can be found by solving the auxiliary quartic equation.
Conclusion
We have achieved the algebraic solution of the general sextic equation. Radical solution of the general sextic equation is possible to achieve. This is a case of violation of Abel’s impossibility theorem and Galois Theory.
Acknowledgements
I would like to express my since gratitude to Almighty God for making this piece of work successful, and my wife, Julie Ahadi, for her encouragement and service.
References
- Adamchik VS, Jeffrey DJ (2003) Polynomial transformations of Tschirnhaus, Bring and Jerrard. ACM SIGSAM Bulletin 37: 90-94.
- Buya SB (2017) The trinomial sextic equation, its algebraic solution by conversion to solvable factorized form. Inter J Applied Sci and Innovations 1: 1-19.
- Buya SB (2017) The general quintic equation, its solution by factorization to cubic and quadratic factors. Inter J Applied Sci and Innovations 1: 29-36.
- E.T. Motlotle (2011) The Bring-Jerrard quintic equation, its solution and a formula for the universal gravitational constant. University of South Africa.
- Cajori F (1991) A history of mathematics. 5th edition, Chelsea Publishing Company, New York, USA.
- Kulkarni RG (2008) Solving sextic equations. Atlantic Electronic J Mathematics 3: 56-60.

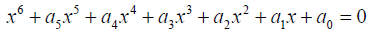 (1)
(1)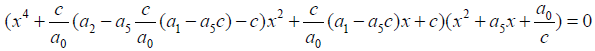 (2)
(2)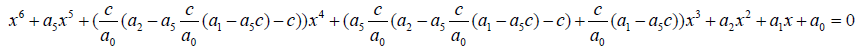 (3)
(3)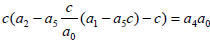 (4)
(4)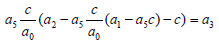 (5)
(5)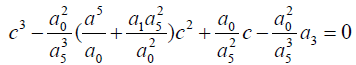 (6)
(6)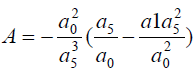 (7)
(7)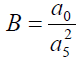 (8)
(8)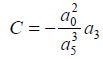 (9)
(9)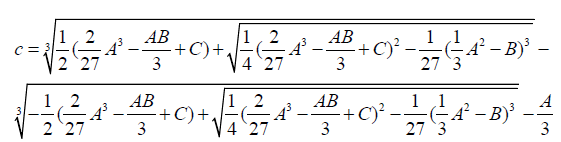 (10)
(10)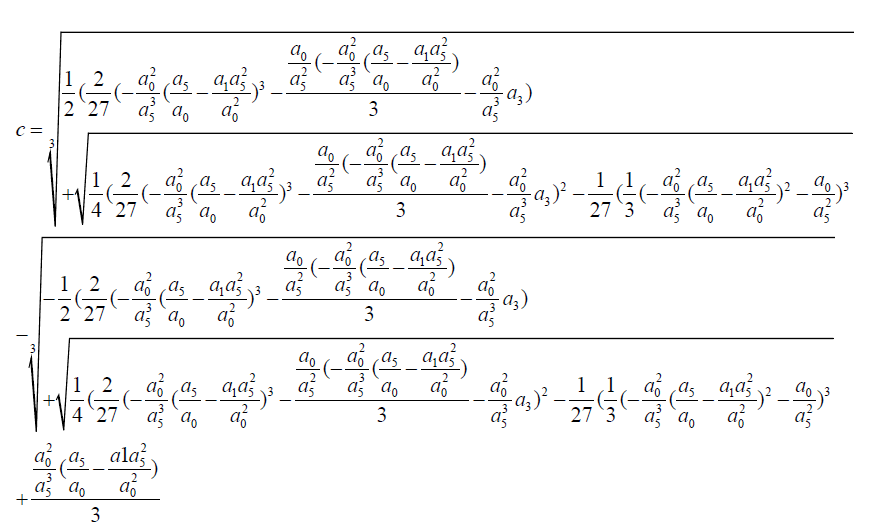 (11)
(11)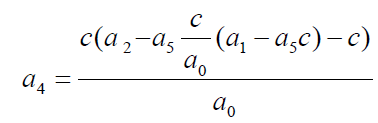 (12)
(12)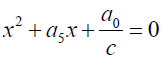
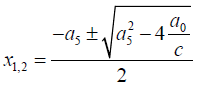
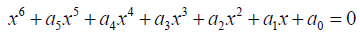 (1)
(1)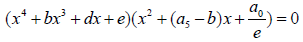 (2)
(2)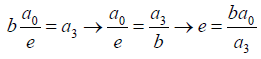 (3)
(3)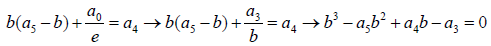 (4)
(4)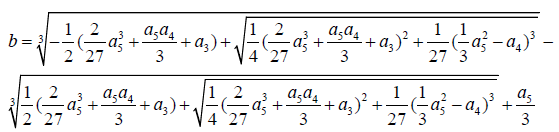 (4)
(4)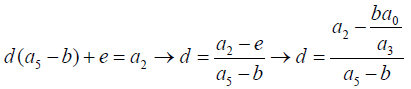 (5)
(5)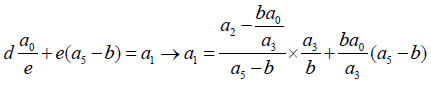 (6)
(6)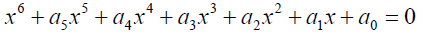 (1)
(1)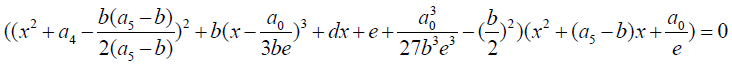 (2)
(2)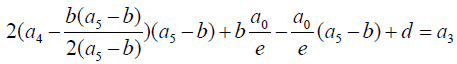 (3)
(3)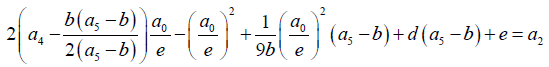 (4)
(4)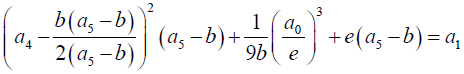 (5)
(5)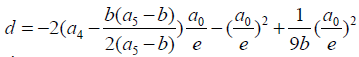 (6)
(6)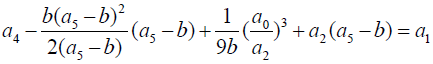
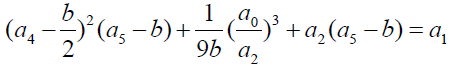 (8)
(8)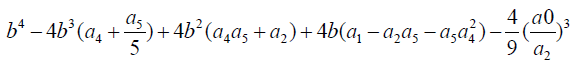 (9)
(9)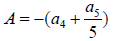 (10)
(10)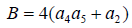 (11)
(11)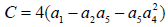 (12)
(12)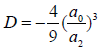 (13)
(13)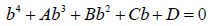 (14)
(14)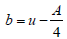 (15)
(15)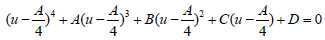 (16)
(16)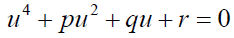 (17)
(17)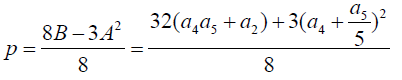 (18)
(18)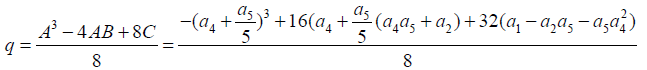 (19)
(19)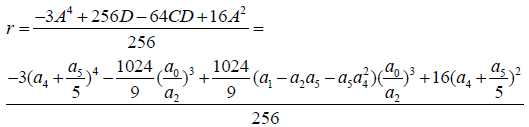 (20)
(20)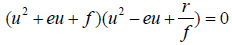 (21)
(21)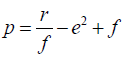 (22)
(22)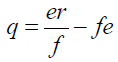 (23)
(23)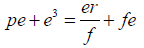 (25)
(25)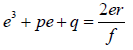 (26)
(26)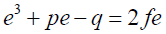 (27)
(27)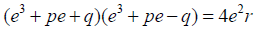 (28)
(28)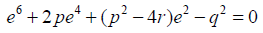 (29)
(29)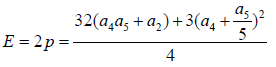 (30)
(30)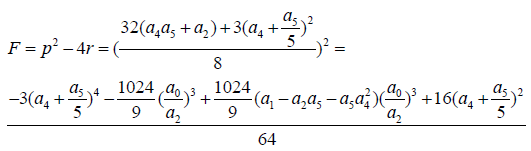 (31)
(31)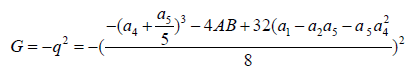 (32)
(32)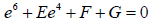 (33)
(33)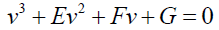 (35)
(35)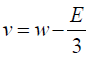 (36)
(36)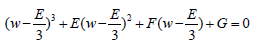 (37)
(37)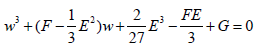 (38)
(38)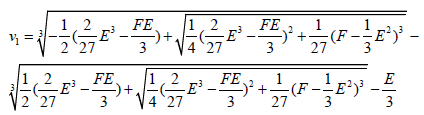 (39)
(39)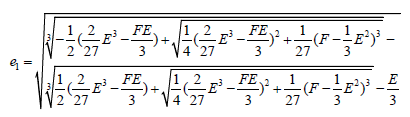 (40)
(40)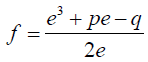 (41)
(41)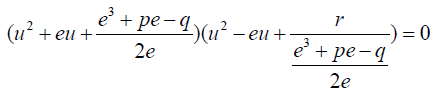 (42)
(42)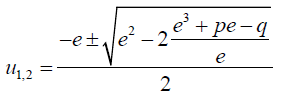 (43)
(43)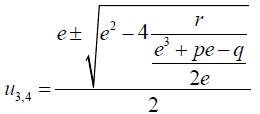 (44)
(44)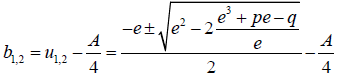 (45)
(45)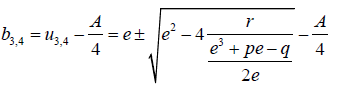 (46)
(46)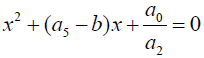 (47)
(47)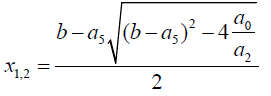 (48)
(48)