European Journal of Experimental Biology Open Access

Keywords

Phospholipase A2; Quercetin; Fluorescence spectroscopy; Molecular modeling

Introduction

Phospholipases A₂ (PLA_2s-E.C. 3.1.1.4) are a large class of intracellular and extracellular enzyme, catalyze the hydrolysis of sn-2 acyl bonds of sn-3-phoapholipids. Intracellular PLA_2s are often membrane associated and are involved in phospholipid metabolism however, extracellular PLA_2s are also found abundantly in the venom of snake and insects [1]. These enzymes are the smallest (~14 kDa), stable, calcium dependent encountered in a wide range of biological fluids, such as saliva, venom, macrophages, platelets, placenta, etc. [2,3]. Naturally occurring PLA₂-homologues in which Asp49 is changed to Lys [4-7], Ser [8] or Ala [9] are therefore catalytically inactive. PLA_2s are highly stable protein due to the presence of disulfide bonds, which help in analysis of biochemical and structural characterization as well as on their pathological effects and other bioactivities. On the basis of amino acid sequence similarities and disulphide bonding pattern, extracellular PLA_2s have been classified into class I, II and III [10].

In particular, extracellular PLA_2s are ubiquitous in nature, represents the major venom component of snakes belonging to genus Bothrops and exhibit a broad range of biological effects including neurotoxicity, myotoxicity, cardiotoxicity, hemolysis, anticoagulant and antiplatelet activities [11-14]. The Phospholipase A₂ (MTX-II), purified from the snake venom Bothrops brazili investigated earlier, a Lys49- PLA_2s that are considered to be catalytically inactive due to their inability to hydrolyze natural phospholipids [15]. For this reason it is important to conduct detailed studies of the microenvironment of binding sites of PLA_2s in order to understand PLA₂–inhibitor interactions. Due to these characteristics, Quercetin (QCT) has been chosen as flavonoid model.

In this work, the interaction of QCT with MTX-II has been investigated in aqueous solutions at three temperatures under physiological conditions. Although there have been a large amount of studies on the interaction of QCT with BSA [16], Ovalbumin [17], Lysozyme [18] however, the binding of QCT with PLA_2s has seldom been reported. Therefore, the main contribution of the present work is to describe the mechanism of interaction between QCT and PLA_2s (MTX-II) at the molecular level.

QCT is one of the widely distributed flavonoids and abundantly found in the flowers and plants as secondary metabolites. They are a large class of naturally occurring bioactive polyphenolic compounds, which have three rings; the basic nucleus of a phenyl benzo (γ)pyrone, that is, two aromatic rings (A and B) joined by a three–carbon linked (γ)-pyrone ring (C), hydroxyl, glycosyl and methoxyl are side groups (Figure 1A) [19]. The flavonoids are poorly water-soluble pigments and are often referred to as “nature’s biological response modifiers”, because of their ability to modify the body’s reaction to allergens, viruses, and carcinogens.

They have attracted considerable attention, specifically because of biological and physiological importance such as modifying eicosanoid biosynthesis, anti-estrogenic, antiprostanoid, anti-inflammatory, antithrombic effect, antihypertensive effect, antiarrhythmic effect, antiviral and carcinostatic properties [20]. A large number of biochemical and molecular biological investigations have shown that therapeutically active flavonoid, both natural and synthetic origin, frequently binds to proteins [21,22]. Therefore, to have a detailed description of the interaction between flavonoid and snake venom toxin at the molecular level is the early stage on the long pipeline of inhibitor design (Figure 1).

Biophysical and computational assays were performed in order to elucidate the binding and the interactions responsible for stabilizing the QCT-MTX-II complex. MTX-II is catalytically inactive due to the presence of Lys-49 in place of Asp-49, in the catalytic site region, but have physiological role such as induce myonectptic effect [23-25], inhibit the vascular endothelial growth factor [26], indicating their biomedical relevance. This would be main emphasis of the current work to get an inhibitor, which affects these physiological roles. Though, in the solution phospholipase (MTX-II) occur in tetramer conformation, but essentially is formed by two dimers as reveled by DLS experiment [15].

The monomers of the tetramer of MTX-II named as A, B, C and D is shown at Figure 1B. In the solution the two dimers formed from monomers of A and B are in the asymmetric unit display different conformation states due to glycosylation by tetraethylene glycol (TTEG), have active site like region. However, the second dimer formed by molecules C and D have an empty active site region. In the all monomers the microenvironments formed by amino acids have eight tyrosines, which distributed on hydrophobic region as well as on the hydrophilic surface and just one tryptophan in between the dimmers interface. Moreover based upon experimental results we also propose, through molecular docking, a structural model for understanding the molecular interactions between MTX-II and QCT.

Materials and Methods

Preparation of stock solutions

PLA2 (MTX-II) was purified from the Brazilian snake; B. brazili venom by Sephacryl S-100 column chromatography [15]. MTX-II was dissolved in Tris-HCl buffer solution of 5 × 10^-2 molL^-1 at pH 8.0, containing 0.10 molL^-1 of sodium chloride. The stock solution of QCT was prepared in ethanol. The QCT stock solution concentration was determined by using an extinction coefficient of 19.95 mM^-1cm^-1 at 257 nm and 21.88 mM^-1 cm^-1 at 376 nm using spectroscopy [27]. The stock solution concentration of QCT was 3.51 × 10^-3 molL^-1.

However, MTX-II stock solution concentration was determined spectroscopically using the extinction coefficient 18.295 M^-1cm^-1 at 280 nm, calculated by ExPASy-ProtParam tool [28] which was 3.21 × 10^-4 molL^-1 by monomer. The structure of QCT and MTX-II has shown in Figure 1A and 1B. A titration experiment was performed by adding small aliquots from QCT stock solution to PLA2 solution at a concentration of 4.0 × 10^-6 molL^-1. The final QCT concentration achieved during the titration was 11 × 10^-6 molL^-1(final ethanol concentration in buffer was <1%).

UV–Vis absorption spectrum

The UV–Vis absorption spectra were obtained by scanning the solution on a Cary-3E spectrophotometer (Varian, Palo Alto, CA) equipped with 1cm quartz cells at room temperature. The UVVis absorbance spectra were recorded in the 200-500 nm range, with an integration time of 0.333 seconds and spectral bandwidth of 2.0 nm. It was performed the baseline subtraction of the buffer for the final spectrum of each solution analyzed.

Fluorescence spectroscopy and titrations

The fluorescence measurements were performed at 288, 298 and 308K using an ISS PC1 steady-state spectrofluorimeter (Champaign, IL, USA) well-appointed with a Neslab RTE-221 thermostat bath. Both excitation and emission bandwidths were set at 4.0 nm. The fluorescence emission spectra were recorded in the range of 290-500 nm follows at excitation at 280 nm. The selected wavelength was chosen because it provides aggregate excitation of tryptophan and tyrosine residues. The emission spectrum was corrected for the background fluorescence of the buffer. The absorbing effect produced by presence of QCT in titration solution was minimized due to its low utilized concentration (up to 11 × 10^-6 molL^-1).

Ab Initio calculation

The Gaussian 09 quantum chemical program series [29] provided by Núcleo de Computação Científica da Universidade Estadual Paulista (NCC/GridUNESP) was used in the calculation of the chemical structure of QCT. The optimized geometry was calculated for the gas phase isolated QCT molecule by using DFT/ B3LYP functional with 6-311+G (d,p) basis set. The vibrational frequency calculation was performed to check if the structures is stable (true minimum on the potential energy surface) whereas no imaginary frequencies should be found. The gap energy between the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) for QCT molecule was calculated, as well as its molecular electrostatic potential (MEP). The NewZMat utility of Gaussian program was used to obtain the PDB file of the QCT molecule.

Molecular modeling calculation

The crystal structure of MTX-II (PDB ID: 4DCF) was obtained from the Protein Data Bank [15]. The 3D structure of the QCT molecule was obtained from Gaussian 09 program series. The AutoDock Tools software [30] of MGL Tools 1.5.4 program was used to prepare MTX-II and QCT by adding polar hydrogen atoms, partial charges and atom types. The ligand rigid root was generated automatically and all possible rotatable bonds and torsions were defined as active. Grid maps were generated with 0.625 Å spacing and dimensions of 82 × 122 × 84 points by the AutoGrid 4.2 program [31] for the whole dimer. The AutoDock 4.2 program was used to study the binding site between QCT and MTX-II by applying the Lamarckian genetic algorithm (LGA) for minimization using default parameters. Random starting positions on the entire protein surface and random orientations were used for the ligand. For each docking simulation, 100 different conformers were generated. The software Pymol [32] was used to visualize the docked conformations and to locate the interactions between QCT and MTX-II.

Results and Discussion

Fluorescence quenching rate constant of PLA₂

Fluorescence quenching is related to any process that reduces the fluorescence intensity of a sample. Quenching can be caused by a variety of molecular interactions such as excited-state reactions, molecular rearrangements, energy transfer, groundstate complex formation, and collisional quenching. Fluorescence quenching can be characterized by two main mechanisms; static and dynamic.

These mechanisms are differentiated one each other due to the response to temperature and viscosity dependent behavior, or preferably with measurements of fluorescence lifetime. Since higher temperature increases diffusion coefficients the bimolecular quenching rate constants follow such increment, because of the enlargement of the collisional quenching extent. In contrast, weakly bounded complexes are dissociated at higher temperature decreasing the quenching rate constant; hence leading to less static quenching [30,33-35].

Fluorescence quenching data was analyzed by the Stern– Volmer equation:

F₀/F=1+ K_qτ₀[Q]=1+ K_sv[Q] (1)

Where F₀ and F are the steady-state fluorescence intensities in the absence and presence of quencher, respectively. In Eq. (1), K_q is the bimolecular quenching constant, τ₀ is the lifetime of the fluorophore in the absence of quencher and its value for MTX-II is 6.05 × 10^-9s [36]. [Q] is the concentration of quencher and K_SVis the Stern–Volmer quenching constant.

In this experiment, the solution concentration of MTX-II was maintained constant at 4.0 × 10^-6 molL^-1 and the QCT concentration varied from 0 to 11 × 10^-6 molL^-1 with increments of 1.0 × 10^-6 molL^-1. The spectra profiles, seen at Figure 2, indicate the contribution of two intrinsic fluorophores species, tyrosine (Tyr) and tryptophan (Trp), due to the presence of two peaks at 305 and 350 nm, respectively [37]. The effect upon fluorescence intensity of MTX-II with the increment of QCT concentration is registered at Figure 2.

As can be seen the fluorescence intensity of MTX-II decreased in the presence of QCT concentrations, indicating that the microenvironments of fluorophores were affected by flavonoid. The spectra profiles also revealed that both peaks (305 and 350 nm) are simultaneously affected and regarding the individual contribution which is different may be due to the microenvironments where they are positioned in the protein. In order to elucidate the response behavior of each contribution at the absence of QCT, a set of experiments at different temperatures were performed. The insert at Figure 2 shows two similar spectra profiles at 288 and 298 K, while at 308 K the peak intensity changed, while at 305 nm the intensity increased at 350 nm it decreased. Certainly such response may be related to the slight conformational changes induced by temperature varying differently the microenvironments where the intrinsic fluorophores are found at MTX-II.

These uneven behaviors may also indicate that the quencher accessibility is different depending on the regions of interaction with MTX-II [33]. As an example, the emission of tryptophan (W68) at 350 nm illustrates that this residue under certain condition is easier exposed to the buffer [33], and which localization is at the dimmer interface [15]. On the other hand, tyrosine with a total of eight residues, taking in account their tridimensional arrangement and the spatial proximity (6-8 Å) are dispersed in three main clusters, the first (Y21, Y24, Y103 and Y107), the second (Y45 and Y51) and the third (Y64 and Y66), shown in Figure S1. In face of major number and spatial distribution, the final emission as a summation do not allow us to infer much about the increment of the signal but confirms that different microenvironments somehow made the quantum efficiency of tyrosines more effective. The results of fluorescence quenching at 288 K, within the concentration range of QCT, are in accordance with the Stern–Volmer equation, which calculus at both wavelength 305 nm and 350 nm obtained the quenching constant (KSV) and which values are presented at (Table 1). It is noticeable that the quenching constant for Trp is a little bit higher than to Tyr, which reinforces our assumption about the solvent accessibility. The same procedure was repeated at 298 K and the quenching constant decreased at both wavelength, and once again showed the same behavior. The Stern-Volmer quenching constant obtained by the slope of linear adjustment and is inversely correlated with temperature is presented at Figure 3. The decrement of the KSVvalues as temperature increases up to 298 K infers that the quenching mechanism of the interaction between MTX-II and QCT is static. In addition, the calculated values in Table 1 show that the binding reaction was greater than 2.0 × 1010 M^-1s-1, the maximum diffusion collision quenching rate constant of various quenchers with biopolymers [38]. Therefore, the fluorescence quenching mechanism of MTX-II-QCT is classified as static quenching process.

Table 1: Stern-Volmer quenching (K_SV), bimolecular quenching constant (K_q), modified Stern-Volmer quenching constant (K_a), binding constant (K_b), and binding site interactions (n) of MTX-II-QCT complex at 288, 298 and 308 K.

At temperature 308 K, Stern-Volmer plot presents a slight negative deviation from linearity (Figure 4). The downward curvature on quenching of MTX-II reflects different accessibilities to the intrinsic fluorophores in protein [33] along the quenching process. This reinforces the conformational changes assumption of the dimer, because the position of the tryptophan residues (W68) at the dimer interface becomes more exposed to the solvent, enhancing their accessibility areas to the quencher when compared to the tyrosines. Thus, the quenching data was analyzed by the modified Stern-Volmer equation at 308 K [39] see the insert at Figure 4.

F₀/ΔF=(faKa)^-1[Q]^-1+fa^-1 (2)

Where ΔF is the difference between the fluorescence intensity in the absence and presence of the quencher at various concentrations [Q], f_a is the fraction of accessible fluorescence and K_a is the effective quenching constant for the accessible fluorophores.

The response between F₀/ΔF and [Q]^-1 is linear, with a slope equal to the value of (f_ak_a)^-1. The value f_a^-1 is fixed on the ordinate. The constant K_a is the quotient between the ordinate and the slope. The fluorescence quenching results analyzed when using Eq. (2) at 308 K is shown in Figure 4. The modified Stern-Volmer constant value was 2.3 × 10⁵ M^-1 and 2.7 × 10⁵ M^-1 at 308 K for Tyr and Trp at 305 and 350 nm, respectively, as shown in Table 1.

Analysis of binding equilibria

In the case of the static quenching mechanism, the assumption adopted is that the binding sites are the same and independent at the protein. For the description of the sitebinding model:

P+nD→D_nP (3)

Where P is the protein (MTX-II), D is the drug (QCT), and D_nP is the new complex molecular which binding constant is K_b. Here K_b is:

K_bⁿ=[D_np]/[P_u][D_u]ⁿ (4)

Considering that all amount of protein and drug is P₀ and D₀, respectively, then [P₀]=[P_u]+[D_nP] and [D₀]=[D_u]+[D_nP], so that the relation between the fluorescence intensity and the unbound protein (P_u) is given by [P_u]/[P₀]=F/F₀ and therefore [40]:

Log(F₀-F)/F=nlogK_b+nlog(1/([D₀]-(F₀-F)[P₀]/F)) (5)

Where K_b is the binding constant for a site and n is the number of binding sites per protein (MTX-II). Figure 5 shows the binding equilibrium plots for the fluorescence quenching of MTX-II by the QCT molecule at 288 and 298 K. The dependence of Log(F₀-F)/F on the value of log(1/([D₀]-(F₀-F)[P₀]/F)) is linear, with a slope equal to the value of n and the value nlogK_b fixed on the ordinate. For the system MTX-II - QCT, K_b and n value at 288 and 298 K are shown in Table 1. It may be observed that the number of binding sites between MTX-II and QCT at 288K is approximately equal to 1.0 (Tyr, 1.3; Trp, 1.2), indicating that there is probability of only one QCT molecule for each MTX-II molecule, in both signals (tyrosine and tryptophan). The data shown in Table 1 indicates that the complex formed at 288 K is more stable than to the complex formed at 298 K. It is also observed that at 288 K the binding constant is magnitude orders higher than the complex at 298 K. This means that the more QCT molecule is carried out if the temperature increases as similar in case of MNP-BSA complex [41]. All the correlation is greater than 0.9 indicating that the interaction between MTX-II and QCT is in good agreement with site binding model. Table 1 also shows the result of K_b decreasing in correlation with the temperature rising, which is in agreement with trends of KSV as mentioned previously (at 288 and 298 K). This fact indicates that the interaction between QCT and MTX-II weakens when the temperature rises, resulting in the reduction of stability of QCTMTX- II complex (static process).

Thermodynamic analysis

The interaction forces between drugs and biomolecules may include electrostatic interaction, multiple hydrogen bonds, van der Waals interactions, hydrophobic and steric contacts within the antibody-binding site, etc. [42]. The thermodynamic parameters, such as enthalpy, entropy and free energy changes are the main evidences to determine the binding mode. Therefore, the thermodynamic parameters depending on temperatures were analyzed in order to better characterize the driving forces between MTX-II and QCT, which were calculated from the van’t Hoff plots.

If the enthalpy changes (ΔH) does not vary significantly within the temperature range, both the enthalpy (ΔH) and entropy (ΔS) changes can be evaluated from the van’t Hoff equation:

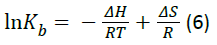
where R is the universal gas constant and K_b is binding constant at the corresponding temperature (T). Table 2 shows the value of ΔH and ΔS obtained from the slopes and ordinates of the van’t Hoff relationship and lists the corresponding value of Gibbs free energy change (ΔG) as calculated from the relation:

Table 2: Thermodynamic parameters of MTX-II-QCT complex at 288 and 298 K and pH 8.0.

ΔG= ΔH-TΔS (7)

The values of entropy and enthalpy changes attained for the binding site from the slopes and ordinates at the origin of the fitted lines are summarized in Table 2. The negative value of Gibbs free energy changes indicates the spontaneity of the binding of QCT with MTX-II. Based on sign and magnitudes of the thermodynamic parameters shown in Table 2, it is possible to discuss the individual type of contribution of the interactions that may occur in the complex MTX-II and QCT. It may be noted that the interaction involving the QCT with MTX-II binding sites is apparently sensitive to temperature. A comparison between enthalpy and entropy change magnitudes will define whether the hydrophobic or the electrostatic contribution will play an important role in the stabilization of the complex. As reported, positive values for both ΔH and ΔS imply typical hydrophobic interaction, while negative values imply the van der Waals forces and hydrogen bonding [16]. Based on studies of water structure, a negative entropy change is generally considered as evidence for hydrophilic interactions and transfer of uncharged hydrophobic molecular form water to macromolecules has generally been considered to be entropic [43].

The entropy and enthalpy change values obtained by the fluorescence quenching intensity which assign the contribution of the amino acids residues Tyr and Trp were negative and summarized in the Table 2. The negative entropy and enthalpy changes arise from non-bonded (Van der Walls) interactions and hydrogen bond formation accompanying association of QCT with MTX-II. Thus hydrogen bonds formed in a low dielectric environment such as parts of the contact areas between MTX-II, which are inaccessible to water or the QCT binding sites in the interior of an enzyme could collectively make a substantial negative contribution to entropy and enthalpy changes [44] as similar in case of interface between the subunits of the α- chymotrypsin dimmer [45] and interaction between S-peptide with the S-protein of Ribonuclease [46]. The estimated result reveals that all the interactions play almost equivalent role in the complex QCT and MTX-II.

Distance measurement between MTX-II and QCT

Fluorescence resonance energy transfer (FRET) is a nondestructive spectroscopic method has been used for measuring molecular distances and relative angular orientation of fluorophores in the biological and macromolecular systems. In general, FRET happens when the emission spectrum of a fluorophore (donor) overlaps with the absorption spectrum of another molecule (acceptor). In addition, according to Förster’s non-radiative energy transfer theory both, the donor and acceptor fluorophores can be totally distinct or close to the same macromolecule and the distance between the donor and acceptor is less than approximately 8.0 nm [47]. According to this theory, the distance r in the binding between MTX-II and QCT can be calculated by the equation:

E=1-F/F₀=R₀⁶/(R₀⁶+r⁶) (8)

where, E is the efficiency of transfer between the donor and the acceptor, r is the average distance between the donor and the acceptor, and R₀ is the critical distance when the transfer efficiency is 50%.

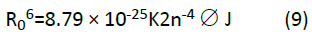
In Eq. (9), K² is the orientation space factor, n is the refracted index of the medium, is the fluorescence quantum yield of the donor, J is the effect of the spectral overlap between the emission spectrum of the donor and the absorption spectrum of the acceptor (Figure 6), which may be calculated by the following equation:

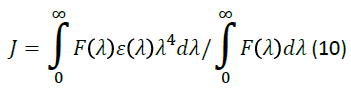
Where, F(λ) is the fluorescence intensity of the fluorescent donor in the wavelength range from λ to λ+Δλ and ɛ(λ) is the extinction coefficient of the acceptor. In order to obtain the distance between the donor (MTX-II) and acceptor (QCT) the concentration of both was 4.0 × 10^-6 molL^-1. In this study, K²=2/3, n=1.36, and ∅=0.093. The ∅ value was calculated by us with the help of a lifetime of the fluorophore as reported by Alcala et al. [48]. According to Eqs. (8)-(10), it was calculated that J=1.791 × 10^-14 cm³Lmol^-1, E=0.084, R₀=2.57 nm and r=3.82 nm. The mean distance between donor and accepter, at which non-radiation transfer can occur, is in the range 2.0-8.0 nm [49], indicating that occur a possible energy transfer from MTX-II to QCT.

Ab Initio calculations

Ab initio calculations were performed using the Gaussian program series 09 provided by Grid UNESP. The optimized geometry was calculated for the gas phase isolated QCT molecule by using B3LYP functional with a 6-311+G(d,p) basis set. Full optimization was performed with no symmetry constraints. The calculated vibrational frequencies verified that the structures were stable (true minimum on the potential energy surface) whereas no imaginary frequencies were obtained. The gap energy value between the HOMO and LUMO molecular orbital is a molecular property and is related to an approximation of the first electronic excitation energy [50-51]. The HOMO–LUMO energy gap of the QCT is about 3.627 eV (ΔE_gap=ΔE_LUMO-ΔE_HOMO), which corresponds to a wavelength of 342 nm. Such wavelength characterizes the HOMO→LUMO transition which is in the range of the absorption spectrum of QCT in aqueous solution (Figure 6). Therefore, the results of ab initio calculation for QCT (in the gas phase) are consistent with the absorption profile band obtained experimentally. Such approach indicates that the optimized geometry is reasonably accepted for the next step of the description of the interaction between QCT and MTX-II. The molecular electrostatic potential (MEP) of QCT (Figure 7) consists basically of the potential energy of a proton test charge at a particular location near a molecule.

In our case, the MEP describes the potentially high positive charge distribution occurs around the A and the B ring of QCT as well have a partial negative charge. The ring C potentially has a high negative charge in comparison to A and B. Therefore, the MEP describes equal charge distribution of QCT, which would interact with MTX-II in the context of electrostatic potential to perform the binding interactions.

Molecular modeling calculations

The crystal structure of MTX-II obtained from the Protein Data Bank (PDB ID: 4DCF) [15]. QCT geometry optimized (in the gas phase) obtained from ab initio calculation were employed to analyze the binding sites of QCT with MTX-II (Figure 8). It shows the result of the two best binding energies out of 100 different conformers generated by the molecular docking. The first and largest cluster is located in between the dimer interface. For the lowest energy pose in this cluster, MTX-II and QCT interacts resulting in energy of -27.8 kcaLmol^-1 and a related binding constant of 7.4 × 10⁴ M^-1, by using the equation:

K=exp(-G_b/RT) (11)

Where, K is the theoretical binding constant, R is the universal gas constant, T is the temperature and G_b is the binding energy. The K value obtained at 298 K in comparison with the experimental value at the same temperature, shown in Table 1, is in good agreement.

The binding site is in the interface region, where W68 of both monomers are in close proximity. However, this conformation is stabilized by three potential hydrogen bonds and three salt bridges between QCT and MTX-II chains. Two hydrogen bonds formed in between the carbonyl oxygen of G14 at chain B and carbonyl oxygen of Q11 at chain A with 4ˈ-OH and 3-OH hydrogen of QCT, respectively. The third hydrogen bond formed in between side chain oxygen of Q11 at chain B with 5-OH hydrogen of QCT. The interaction is also stabilized by three salt bridges; two salt bridges formed with single esoteric oxygen of γ-pyrone ring C of QCT with carboxyl oxygen of Q11 at chain A and side chain oxygen of Q11 at chain B of MTX-II, respectively. The third salt bridge formed from oxygen of 3ˈ-OH of QCT with ζ –NH3+ (amino group) hydrogen of Lys 7.

The second largest cluster is situated within the active site like region formed by helix H1 and H2. The lowest energy pose in this cluster is -25.8 kJmol^-1 resulting in a theoretical binding constant of 3.4 × 10⁴ M^-1. This conformation is stabilized by three potential hydrogen bonds and one salt bridge. The hydrogen bonds occur in between carbonyl oxygen of P17, G29 and C44 of MTX-II with 7-OH, 3ˈ-OH and 3-OH hydrogen of QCT, respectively. The QCT binding in the active site like region are supported by salt bride in between 3-OH oxygen of QCT with δ1- NH hydrogen of His 47. The salt bridge formed with H47, which can be responsible for a physiological role of MTX-II, so this result inform that QCT can be used as an inhibitor for MTX-II. The two binding sites found in docking analysis are assumed to be present in Phospholipase A2. This is in line with the results achieved by Ohno et al. [52] about the secreted Phospholipases.

Conclusion

In this paper, the interaction of QCT with MTX-II has been investigated in vitro as well as in combination with ab initio and molecular modeling calculations. These assays indicate that QCT can bind to MTX-II in between the dimer interface and to the active site like region. The most probable quenching mechanism for the interaction between QCT and MTX-II is static process, due to the cutback on the Stern-Volmer quenching constant (KSV) up to temperature 298K, but at 308K the fluorescence quenching process reflects the difference of accessibility of the quenchers to the intrinsic fluorophores. The thermodynamics parameters indicates that the interaction is spontaneous (ΔG<0), and negative entropy and enthalpy data support hydrogen bond formation. The distance (r) between donor and acceptor is obtained according to Forster non-radioactive energy theory (FRET). Spectroscopic experiments and molecular modeling assays indicated that hydrophobic surface supports binding of QCT at two different sites. The binding study of QCT to MTX-II is of great importance to understand chemical-biological interactions for future drug design, pharmacology, and biochemistry studies. Furthermore, these assays are expected to provide more information about the interactions of the protein MTX-II with natural product in view of an application as a therapeutic drug.

Acknowledgements

The authors would like to acknowledge the financial assistance from CAPES/CNPq/CNPq in the form of research fellowship to RK/IPC/AU respectively. Financial assistance from FAPESP and TWAS also acknowledged.

References

1. Arni RK, Ward RJ (1996) Phospholipase A2-A structural review. Toxicon 34: 827-841.
2. Van Deenem LLM, de Haas GH (1963) The substrate specificity of phospholipase A2. Biochem Biophys Acta. 70:538-553.
3. Waite M (1990) Phospholipase, enzymes that share a substrate class. Adv Exp Med Biol 279: 1-22.
4. Maraganore JM, Merutka G, Cho W, Welches W, Kezdy FJ, et al. (1984) A new class of phospholipase A2 with lysine in place of aspartate. J Biol Chem 259: 13839-13843.
5. Francis B, Gutierrez JM, Lomonte B, Kaiser II (1991) Myotoxin II from Bothrops asper (Terciopelo) venom is a lysine 49 phospholipase A2. Arch Biochem Biophys 284: 352-359.
6. Homsi-Brandenburgo MI, Queiroz LS, Santo-Neto H, Rodrigues-Simoni L, Giglio JR (1988) Fractionation of Bothrops juraracussu snake venom: partial chemical characterization and biological activity of bothropstoxin. Toxicon 26: 615-627.
7. Ward RJ, Monesi N, Arni RK, Larson RE, Paco-Larson ML (1995) Sequence of a cDNA encoding bothropstoxin I, a myotoxin from the venom of Bothrops jararacuss. Gene 156: 305-306.
8. Krizaj I, Bieber AL, Ritonja A, Gubensek F (1991) The primary structure of ammodytin L, a myotoxic phospholipase A2 homologue from Viperu ammodytes. Venom. Eur J Biochem 202: 1165-68.
9. Liu CS, Chen JM, Chang CH, Chen SW, Teng CM, et al. (1991) The amino acid sequence and properties of an edema-inducing Lys-49 phospholipase A2 homolog from the venom of Trimeresus mucrosquamatus. Biochem Biophys Acta 1071:362-370.
10. Renetseder R, Brunie S, Dijkstra BW, Drenth J, Sigler PB (1985) A comparison of the crystal structures of phospholipase A2 from bovine pancreas and Crotulus utrox venom. J Biol Chem 260: 11627-11636.
11. Chwetzoff S, Tsunasawa S, Sakiyama F, Menez A, Nigexine (1989) A phospholipase A2 from cobra venom with cytotoxic properties not related to esterase activity. Purification, amino acid sequence, and biological properties. J Biol Chem 264: 13289-13297.
12. Kini RM (2005) Structure-function relationship and mechanism of anticogulant phospholipase A2 enzymes. Toxicon 45: 1147-1161.
13. Schaloske RH, Dennis EA (2006) The phospholipase A2 superfamily and its group numbering system. Biochim Biophys Acta 1761: 1246-1259.
14. Kang TS, Georgieva D, Genov N, Murakami MT, Sinha M, et al. (2011) Enzymatic toxins from snake venom: structural characterization and mechanism of catalysis. FEBS J 278: 4544-4576.
15. Ullah A, Souza TA, Betzel C, Murakami MT, Arni RK (2012) Crystallographic portrayal of different conformational states of a Lys49 phospholipase A₂ homologue: insights into structural determinants for myotoxicity and dimeric configuration. Int J Biol Macromol 51: 209-214.
16. Caruso IP, Vilegas W, Fossey MA, Cornelio ML (2012) Exploring the binding mechanism of Guaijaverin to human serum albumin: fluorescence spectroscopy and computational approach. Spectrochem Acta A 97: 449-455.
17. Lu Y, Wang YL, Gao SH, Wang GK, Yan CL, et al. (2009) Interactions of quercetin with ovalbumin: Spectroscopic and molecular modeling studie. J Luminescence 129: 1048-1054.
18. Wang GK, Wang LX, Tang W, Hao XX, Wang YL, et al. (2011)Binding of quercetin to lysozyme as probed by spectroscopic analysis and molecular simulation. J Fluorescence 21: 1879-1886.
19. Morand C, Crespy V, Manach C, Besson C, Demigne C, et al. (1998) Plasma metabolites of quercetin and their antioxidant properties. Am J Physiol 275: 212-219.
20. Formica JV, Regelson W (1995) Review of the biology of quercetin and related bioflavonoids. Food Chem Toxicol 33: 1061-1080.
21. Kaldas MI, Walle UK, Van der Woude H, McMillan JM, Walle T (2005) Covalent binding of the flavonoid quercetin to human serum albumin. J Agric Food Chem 53: 4194-4197.
22. Kanakis CD, Tarantilis PA, Polissiou MG, Diamantoglou S, Tajmir-Riahi HA (2006)Antioxident flavonoids bind human sérum albumin. J Mol Struct 798: 69-74.
23. Lomonte B, Tarkaowski A, Hanson LA (1993) Host response to Bothrops asper snake venom. Analysis of edema formation, inflammatory cells, and cytokine release in a mouse model. Inflammation 17: 93-105.
24. Lomonte B, Lundgren J, Johansson B, Bagge U (1994) The dyanamics of local tissue damage inducecd by Bothropus asper snake venom and myotoxin II on th mouse cremaster muscle: An intreavital and electron microscopic study. Toxicon 32: 41-55.
25. Lomonte B, Moreno E, Tarkowski A, Hanson LA, Maccarana M (1994) Neutralizing interactionbetween heparins and myotoxin 11, a lysine 49 phosphohpase A2 from Bothrops asper snake venom. J Biol Chem 269: 29867-29873.
26. Yamazaki Y, Matsunaga Y, Nakano Y, Morita T (2005) Identification of vascular endothelial growth factor receptor-binding protein in the venom of eastern cottonmouth. A new role of snake venom myotoxic Lys49-phospholipase A2. J Biol Chem 280: 29989-29992.
27. https://www.sigmaaldrich.com/etc/medialib/docs/Sigma/Product_Information_Sheet/1/q0125pis.Par.0001.File.tmp/q0125pis.pdf
28. Gattiker A, Gasteiger E, Hoogland C, Duvaud S, Wilkins MR, et al. (2005) Bairoch, Protein Identification and Analysis Tools on the ExPASy Server;
    (In) John M. Walker (ed): The Proteomics Protocols Handbook, Humana Press.
29. Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, et al. (1998) Gaussian 98, Revision A. 9 Gaussian, Inc., Pittsburgh, PA.
30. Sanner MF (1999) Python: a programming language for software integration and development. J Mol Graph Model 17: 57-61.
31. Morris GM, Goodsell DS, Halliday RS, Huey R, Hart WE, et al. (1998) Automated docking using a Larmarckian genetic algorithm and an empirical binding free energy function. J Comput Chem 19: 1639-1662.
32. Delano WL (2004) PyMOL software, version 0.99, USA, San Carlos.
33. Lokowicz JR (1999) Principles of fluorescence spectroscopy, second ed., Kluwer academic publishers/plenum press, New York.
34. Hu YJ, Li W, Liu Y, Dong JX, Qu SS (2005) Fluorometric investigation of the interaction between methylene blue and human serum albumin. J Pharm Biomed Anal 39: 740-745.
35. Hu YJ, Liu Y, Wang JB, Xiao XH, Qu SS (2004) Study of the interactions between monammonium glycyrrhizinate and bovine serum albumin. J Pharm Biomed Anal 36: 915-919.
36. Liu EH, Qi LW, Li P (2010) Structural relationship and binding mechanisms of five flavonoids with bovine serum albumin. Molecules 15: 9092-9103.
37. Abou-Zied OK, Al-Shihi OI (2008) Characterization of subdomain IIA binding site of human serum albumin in its native, unfolded, and refolded states using small molecular probes. J Am Chem Soc 130: 10793-10801.
38. Wells TA, Nakazawa M, Manabe K, Song PS (1994) A conformational change associated with the phototransformation of pisum phytochrome A as probe by fluorescence quenching. Biochemistry 33: 708-712.
39. Ware WR (1962) Oxygen quenching of fluorescence in solution: an experimental study of the diffusion process. J Phys Chem 66: 455-458.
40. Bi S, Ding L, Tian Y, Song D, Zhou X, et al. (2004) Investigation of the interaction between flavonoids and human serum albumin. J Mol Struct 703: 37-45.
41. Seelig J, Ganz P (1991) Nonclassical hydrophobic effect in membrane binding equilibria. Biochemistry 30: 9354-9359.
42. Lehrer SS (1971) Solute perturbation of protein fluorescence. The quenching of the tryptophan fluorescence of model compounds and of lysozyme by iodide ion. Biochemistry 10: 3254-3263.
43. Leckband D (2000) Measuring the forces that control protein interactions. Annu Rev Biophys Biomol Struct 29: 1-26.
44. Ross PD, Subramanian S (1981) Thermodynamics of protein association reactions: forces contributing to stability. Biochemistry 20: 3096-3102.
45. Vandlen RL, Tulinsky A (1973) Changes in the tertiary structure of alpha-chymotrypsin with change in pH: p4 4.2-6.7. Biochemistry 12: 4193-4200.
46. Wyckoff HW, Tsernoglou D, Hanson AW, Knox JR, Lee B, et al. (1970) The three-dimensional structure of ribonuclease-S. Interpretations of an electron density map at a nominal resolution of 2 A. J Biol Chem245: 305-328.
47. Weiss S (1999) Fluorescence spectroscopy of single biomolecules. Science 283: 1676-83.
48. Alcala JR, Gratton E, Prendergast FG (1987) Interpretation of fluorescence decays in proteins using continuous lifetime distributions. J Biophy 51: 925-936.
49. Pan BF, Gao F, Ao LM (2005) Investigation of interactions between dendrimer-coated magnetite nanoparticles and bovine serum albumin. J Magn Magn Mater 293: 252-258.
50. Verheij H, Volwerk J, Jansen E, Puyk W, Dijisktra B, et al. (1980) Methylene of histdine-48 in pancreatic phospholipase A2. Role of histidine an calcium ion in the catalytic mechanism. Biochemistry 19: 743-750.
51. Scott D, Sigler P (1994) Structure and catalytic mechanism of secretory phospholipase A2. Adv Protein Chem 45: 53-88.
52. Ohno M, Chijiwa T, Oda-Ueda N, Ogawa T, Hattori S (2003) Molecualar evolution of myotoxic phospholipase A2 from snake venom. Toxicon 42: 841-854.